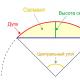
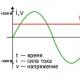
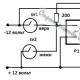
Prečni upogib nosilca. Ravni zavoj ravno prečni zavoj. Primer ravnega upogibnega problema - računski diagram

V tehniki in gradbeništvu (trdnost materialov, konstrukcijska mehanika, teorija trdnosti) nosilec razumemo kot element nosilne konstrukcije, ki je dovzeten predvsem za upogibne obremenitve in ima različne oblike preseka.

Seveda so v realni gradnji nosilne konstrukcije podvržene tudi drugim vrstam obremenitev (obremenitev vetra, vibracije, izmenična obremenitev), vendar se glavni izračun vodoravnih, večpodprtih in togo pritrjenih nosilcev izvaja pod vplivom bodisi nanjo zmanjšana prečna ali enakovredna obremenitev.

Računska shema obravnava žarek kot togo pritrjeno palico ali kot palico, nameščeno na dveh nosilcih. Če so nosilci 3 ali več, se palični sistem šteje za statično nedoločen in izračun upogiba tako celotne konstrukcije kot njenih posameznih elementov postane bistveno bolj zapleten.

V tem primeru se glavna obremenitev obravnava kot vsota sil, ki delujejo v smeri, pravokotni na odsek. Namen izračuna upogiba je določiti največji upogib (deformacijo), ki ne sme presegati mejnih vrednosti in označuje togost tako posameznega elementa (kot celotne z njim povezane gradbene konstrukcije).

Osnovne določbe računskih metod

Sodobne konstrukcijske metode za izračun trdnosti in togosti paličnih (nosilnih) konstrukcij omogočajo že v fazi načrtovanja določitev vrednosti upogiba in sklepanje o možnosti delovanja gradbene konstrukcije.

Izračun togosti nam omogoča, da rešimo vprašanje največjih deformacij, ki se lahko pojavijo v gradbeni konstrukciji pod kompleksnim delovanjem različnih vrst obremenitev.

Sodobne metode izračuna, izvedene s pomočjo specializiranih izračunov na elektronskih računalnikih ali izvedene s pomočjo kalkulatorja, omogočajo določitev togosti in trdnosti raziskovalnega predmeta.

Kljub formalizaciji računskih metod, ki vključujejo uporabo empiričnih formul, vpliv realnih obremenitev pa upoštevamo z uvedbo korekcijskih faktorjev (varnostnih faktorjev), celovit izračun dokaj polno in ustrezno oceni obratovalno zanesljivost zgrajene konstrukcije oz. izdelani element stroja.

Kljub ločenosti izračunov trdnosti in določanja togosti konstrukcije sta obe metodi med seboj povezani, pojma "togost" in "trdnost" pa sta neločljiva. Vendar pa pri strojnih delih pride do glavnega uničenja objekta zaradi izgube trdnosti, medtem ko so objekti konstrukcijske mehanike pogosto neprimerni za nadaljnjo uporabo zaradi znatnih plastičnih deformacij, ki kažejo na nizko togost konstrukcijskih elementov ali objekta kot celote.

Danes sta v disciplinah "Trdnost materialov", "Strukturna mehanika" in "Strojni deli" sprejeti dve metodi izračuna trdnosti in togosti:

1. Poenostavljeno(formalno), med katerim se v izračunih uporabljajo agregirani koeficienti.
2. Rafinirano, kjer se ne uporabljajo samo varnostni faktorji, ampak se na podlagi mejnih stanj izračuna tudi kontrakcija.

Algoritem za izračun togosti

Formula za določanje upogibne trdnosti žarka

• M– največji moment, ki se pojavi v žarku (določeno iz momentnega diagrama);
• Wn, min– moment upora odseka (najdemo iz tabele ali izračunamo za dani profil), odsek ima običajno 2 uporna momenta odseka, Wx se uporablja pri izračunih, če je obremenitev pravokotna na x-x os profila ali Wy, če je obremenitev pravokotna na os y-y;
• Ry– konstrukcijska odpornost jekla na upogibanje (nastavljena glede na izbiro jekla);
• γc– koeficient delovnih pogojev (ta koeficient je v tabeli 1 SP 16.13330.2011);

Algoritem za izračun togosti (določitev količine upogiba) je precej formaliziran in ga ni težko obvladati.

Za določitev odklona žarka je potrebno izvesti naslednje korake v spodnjem zaporedju:

1. Sestavite shemo izračuna predmet raziskovanja.
2. Določite dimenzijske značilnosti tramovi in ​​oblikovalski odseki.
3. Izračunajte največjo obremenitev, ki deluje na žarek in določa točko njegove uporabe.
4. Če je potrebno, žarek (v konstrukcijski shemi ga bo nadomestila breztežna palica) dodatno preverimo na trdnost z največjim upogibnim momentom.
5. Določi se vrednost največjega upogiba, ki označuje togost žarka.

Če želite sestaviti načrt zasnove žarka, morate vedeti:

1. Geometrijske dimenzije žarka, vključno z razponom med nosilci, in če obstajajo konzole, njihovo dolžino.
2. Geometrijska oblika in dimenzije prečnega prereza.
3. Naloži naravo in njihove točke uporabe.
4. Material žarka ter njegove fizikalne in mehanske lastnosti.

Pri najpreprostejšem izračunu dvopodpornih nosilcev se ena podpora šteje za togo, druga pa je tečajna.

Določanje vztrajnostnih momentov in upora prereza

Geometrijske značilnosti, ki so potrebne pri izračunu trdnosti in togosti, vključujejo vztrajnostni moment preseka (J) in uporni moment (W). Za izračun njihovih vrednosti obstajajo posebne formule za izračun.

Formula modula odseka

Pri določanju vztrajnostnih in upornih momentov je potrebno paziti na orientacijo prereza v ravnini reza. S povečanjem vztrajnostnega momenta se poveča togost nosilca in zmanjša upogib. To lahko enostavno preverimo v praksi tako, da desko poskusimo upogniti v običajni, »ležeči« položaj in jo položimo na rob.

Določitev največje obremenitve in upogiba

Formula za določanje upogiba

• q– enakomerno porazdeljena obremenitev, izražena v kg/m (N/m);
• l– dolžina žarka v metrih;
• E– modul elastičnosti (za jeklo enako 200-210 GPa);
• jaz– vztrajnostni moment preseka.

Pri določanju največje obremenitve je treba upoštevati precejšnje število dejavnikov, ki delujejo tako stalno (statične obremenitve) kot občasno (veter, udarna obremenitev z vibracijami).

V enonadstropni hiši bo leseni nosilec stropa izpostavljen stalnim silam teže zaradi lastne teže, predelnih sten v drugem nadstropju, pohištva, stanovalcev itd.

Značilnosti izračunov upogibov

Seveda se izračun talnih elementov za odklon izvaja za vse primere in je obvezen ob prisotnosti znatne ravni zunanjih obremenitev.

Danes so vsi izračuni vrednosti upogiba precej formalizirani in vse zapletene realne obremenitve so zmanjšane na naslednje preproste računske sheme:

1. Jedro, ki počiva na fiksnem in zgibnem nosilcu, ki zaznava koncentrirano obremenitev (primer je obravnavan zgoraj).
2. Jedro, ki leži na fiksni in zgibni konstrukciji, na katero deluje porazdeljena obremenitev.
3. Različne možnosti nalaganja togo pritrjena konzolna palica.
4. Delovanje na konstrukcijski objekt kompleksne obremenitve– porazdeljen, koncentriran, upogibni moment.

Hkrati metoda in algoritem izračuna nista odvisna od materiala izdelave, katerega trdnostne lastnosti se upoštevajo z različnimi vrednostmi modula elastičnosti.

Najpogostejša napaka je običajno premajhno štetje merskih enot. Na primer, faktorji sile se nadomestijo v formulah za izračun v kilogramih, vrednost modula elastičnosti pa se vzame v skladu s sistemom SI, kjer ni pojma "kilogram sile", vse sile pa se merijo v newtonih ali kilonewtonih.

Vrste žarkov, ki se uporabljajo v gradbeništvu

Sodobna gradbena industrija pri gradnji industrijskih in stanovanjskih objektov uporablja palične sisteme različnih presekov, oblik in dolžin, izdelane iz različnih materialov.

Najbolj razširjeni so jekleni in leseni izdelki. Odvisno od uporabljenega materiala ima določanje vrednosti upogiba svoje nianse, povezane s strukturo in enakomernostjo materiala.

Lesena

Sodobna nizka gradnja individualnih hiš in podeželskih hiš obsežno uporablja hlode iz mehkega in trdega lesa.

V bistvu se leseni izdelki, ki delujejo na upogibanje, uporabljajo za ureditev tal in stropov. Prav ti strukturni elementi bodo imeli največje bočne obremenitve, kar bo povzročilo največji odklon.

Upogib lesenega hloda je odvisen od:

1. Iz materiala(vrsta lesa), ki je bil uporabljen za izdelavo trama.
2. Iz geometrijskih značilnosti in obliko prereza predmeta oblikovanja.
3. Od kumulativnega delovanja različne vrste obremenitev.

Merilo za dopustnost odklona žarka upošteva dva dejavnika:

1. Ujemanje z resničnim odklonom največje dovoljene vrednosti.
2. Možnost uporabe strukture ob prisotnosti izračunanega upogiba.

Jeklo

Imajo bolj zapleten prerez, ki je lahko sestavljen, izdelan iz več vrst valjane kovine. Pri izračunu kovinskih konstrukcij je poleg določanja togosti samega predmeta in njegovih elementov pogosto potrebno določiti trdnostne značilnosti povezav.

Običajno se povezava posameznih elementov jeklene konstrukcije izvede:

1. Z uporabo navojev(čepi, vijaki in vijačne) povezave.
2. Povezava z zakovicami.

Upogibna deformacija sestoji iz ukrivljenosti osi ravne palice ali v spremembi začetne ukrivljenosti ravne palice (slika 6.1). Spoznajmo osnovne pojme, ki se uporabljajo pri obravnavi upogibne deformacije.

Palice, ki se upognejo, se imenujejo tramovi.

čisto imenovano upogibanje, pri katerem je upogibni moment edini faktor notranje sile, ki nastane v prečnem prerezu nosilca.

Pogosteje se v prerezu palice poleg upogibnega momenta pojavi tudi prečna sila. Ta upogib se imenuje prečni.

Ravno (ravno) imenujemo upogib, ko ravnina delovanja upogibnega momenta v prerezu poteka skozi eno od glavnih središčnih osi prereza.

pri poševni ovinek ravnina delovanja upogibnega momenta seka prerez žarka vzdolž črte, ki ne sovpada z nobeno od glavnih središčnih osi prereza.

Študijo upogibne deformacije začnemo s primerom čistega ravninskega upogiba.

Normalne napetosti in deformacije med čistim upogibom.

Kot je bilo že omenjeno, je pri čistem ravninskem upogibu v prečnem prerezu od šestih faktorjev notranje sile le upogibni moment različen od nič (slika 6.1, c):

Poskusi, izvedeni na elastičnih modelih, kažejo, da če se na površino modela nanese mreža črt (slika 6.1, a), se s čistim upogibom deformira na naslednji način (slika 6.1, b):

a) vzdolžne črte so ukrivljene vzdolž oboda;

b) obrisi prerezov ostanejo ravni;

c) konturne črte odsekov se povsod sekajo z vzdolžnimi vlakni pod pravim kotom.

Na podlagi tega se lahko domneva, da pri čistem upogibanju ostanejo prečni prerezi nosilca ravni in se vrtijo tako, da ostanejo normalni na ukrivljeno os nosilca (ravni odseki v hipotezi o upogibanju).

riž. 6.1

Z merjenjem dolžine vzdolžnih črt (slika 6.1, b) lahko ugotovite, da se zgornja vlakna podaljšajo, ko se žarek upogne, spodnja pa se skrajšajo. Očitno je mogoče najti vlakna, katerih dolžina ostane nespremenjena. Niz vlaken, ki ne spremenijo svoje dolžine, ko je žarek upognjen, se imenuje nevtralna plast (n.s.). Nevtralna plast seka prečni prerez žarka v ravni črti, ki se imenuje odsek nevtralne črte (n.l.)..

Za izpeljavo formule, ki določa velikost normalnih napetosti, ki nastanejo v prečnem prerezu, upoštevajte odsek nosilca v deformiranem in nedeformiranem stanju (slika 6.2).

riž. 6.2

Z dvema infinitezimalnima presekoma izberemo element dolžine
. Pred deformacijo odseki, ki omejujejo element
, so bili vzporedni drug z drugim (slika 6.2, a), po deformaciji pa so se rahlo upognili in tvorili kot
. Dolžina vlaken, ki ležijo v nevtralni plasti, se pri upogibanju ne spremeni
. Polmer ukrivljenosti sledi nevtralne plasti na risalni ravnini označimo s črko . Določimo linearno deformacijo poljubnega vlakna
, ki se nahaja na daljavo iz nevtralne plasti.

Dolžina tega vlakna po deformaciji (dolžina loka
) je enako
. Glede na to, da so imela pred deformacijo vsa vlakna enako dolga
, ugotovimo, da je absolutni raztezek obravnavanega vlakna

Njegova relativna deformacija

To je očitno
, saj se dolžina vlakna, ki leži v nevtralni plasti, ni spremenila. Potem po zamenjavi
dobimo

(6.2)

Zato je relativna vzdolžna deformacija sorazmerna z oddaljenostjo vlakna od nevtralne osi.

Naj uvedemo predpostavko, da pri upogibanju vzdolžna vlakna ne pritiskajo druga na drugo. Pod to predpostavko se vsako vlakno deformira ločeno, pri čemer doživi preprosto napetost ali stiskanje, pri čemer
. ob upoštevanju (6.2)

, (6.3)

to pomeni, da so normalne napetosti neposredno sorazmerne z oddaljenostjo točk prečnega prereza od nevtralne osi.

Zamenjajmo odvisnost (6.3) v izraz za upogibni moment
v prerezu (6.1)

.

Spomnimo se, da je integral
predstavlja vztrajnostni moment preseka glede na os

.

(6.4)

Odvisnost (6.4) predstavlja Hookov zakon za upogib, saj povezuje deformacijo (ukrivljenost nevtralne plasti).
) s trenutkom, ki deluje v odseku. delo
se imenuje togost preseka med upogibanjem, N m 2.

Zamenjajmo (6.4) v (6.3)

(6.5)

To je zahtevana formula za določanje normalnih napetosti med čistim upogibanjem nosilca na kateri koli točki njegovega prečnega prereza.

Da bi ugotovili, kje v prečnem prerezu se nahaja nevtralna črta, v izraz za vzdolžno silo nadomestimo vrednost normalnih napetosti.
in upogibni moment

Zaradi
,

;

(6.6)

(6.7)

Enačba (6.6) kaže, da je os – nevtralna os prereza – poteka skozi težišče prereza.

Enakost (6.7) to pokaže in - glavne središčne osi prereza.

Po (6.5) je najvišja napetost dosežena v vlaknih, ki so najbolj oddaljena od nevtralne črte

Odnos predstavlja osni uporni moment preseka glede na njegovo središčno os , Pomeni

Pomen za najpreprostejše prereze naslednje:

Za pravokoten prerez

, (6.8)

Kje - stran odseka pravokotna na os ;

- stran odseka vzporedna z osjo ;

Za okrogel prerez

, (6.9)

Kje - premer krožnega preseka.

Trdnostni pogoj za normalne upogibne napetosti lahko zapišemo v obliki

(6.10)

Vse dobljene formule so bile pridobljene za primer čistega upogiba ravne palice. Delovanje prečne sile vodi v dejstvo, da hipoteze, na katerih temeljijo zaključki, izgubijo svojo moč. Vendar pa računska praksa kaže, da tudi pri prečnem upogibanju nosilcev in okvirjev, ko so v prerezu, poleg upogibnega momenta
obstaja tudi vzdolžna sila
in strižna sila , lahko uporabite formule, podane za čisto upogibanje. Napaka je nepomembna.

Pri izračunu trdnosti upogibnih elementov gradbenih konstrukcij se uporablja metoda izračuna mejnega stanja.

V večini primerov so normalne napetosti v prerezih najpomembnejše pri ocenjevanju trdnosti nosilcev in okvirjev. V tem primeru najvišje normalne napetosti, ki delujejo v najbolj oddaljenih vlaknih nosilca, ne smejo preseči določene dovoljene vrednosti za dani material. Pri metodi izračuna mejnega stanja je ta vrednost enaka konstrukcijski upornosti R, pomnoženo s koeficientom delovnih pogojev na vasi

Pogoj trdnosti ima naslednjo obliko:

Vrednote R in y s za različne materiale so podani v SNiP za gradbene konstrukcije.

Za nosilce iz plastičnega materiala, ki je enako odporen na napetost in stiskanje, je priporočljivo uporabiti odseke z dvema simetričnima osema. V tem primeru je pogoj trdnosti (7.33), ob upoštevanju formule (7.19), zapisan v obliki

Včasih se zaradi konstrukcijskih razlogov uporabljajo nosilci z asimetričnim prečnim prerezom, kot so T-nosilec, I-nosilec z več prirobnicami itd. V teh primerih je pogoj trdnosti (7.33) ob upoštevanju (7.17) zapisan v obliki

V formulah (7.34) in (7.35) W z in WHM- presečni uporni momenti glede na nevtralno os Oz“ Mnb je največji upogibni moment v absolutni vrednosti zaradi delovanja projektiranih obremenitev, tj. ob upoštevanju koeficienta zanesljivosti obremenitve y^.

Odsek žarka, v katerem deluje največja absolutna vrednost upogibnega momenta, se imenuje nevaren odsek.

Pri izračunu trdnosti strukturnih elementov, ki delujejo pri upogibanju, se rešujejo naslednji problemi: preverjanje trdnosti žarka; izbira odseka; določitev nosilnosti (nosilnosti) nosilca, tiste. določitev vrednosti obremenitve, pri katerih največje napetosti v nevarnem delu žarka ne presegajo vrednosti y c R.

Rešitev prvega problema se nanaša na preverjanje izpolnjevanja trdnostnih pogojev pri znanih obremenitvah, obliki in dimenzijah preseka ter lastnostih materiala.

Rešitev drugega problema se zmanjša na določitev dimenzij odseka dane oblike pri znanih obremenitvah in lastnostih materiala. Najprej se iz pogojev trdnosti (7.34) ali (7.35) določi vrednost zahtevanega upornega momenta

in nato se nastavijo dimenzije odseka.

Za valjane profile (I-žarki, kanali) na podlagi momenta upora se prečni prerez izbere glede na sortiment. Za nevaljane odseke so določene značilne mere odsekov.

Pri reševanju problema določanja nosilnosti žarka najprej iz pogojev trdnosti (7.34) ali (7.35) vrednost največjega izračunanega upogibnega momenta najdemo s formulo

Nato se upogibni moment v nevarnem odseku izrazi v smislu obremenitev, ki delujejo na nosilec, in ustrezne vrednosti obremenitve se določijo iz nastalega izraza. Na primer, za jekleni I-nosilec 130, prikazan na sl. 7.47, ob R= 210 MPa, y c = 0,9, W z= 472 cm 3 najdemo

Iz diagrama upogibnih momentov najdemo

riž. 7.47

V nosilcih, obremenjenih z velikimi koncentriranimi silami, ki se nahajajo blizu nosilcev (slika 7.48), je lahko upogibni moment M nb relativno majhen, strižna sila 0 nb v absolutni vrednosti pa je lahko pomembna. V teh primerih je treba preveriti trdnost nosilca z najvišjimi tangencialnimi napetostmi tnb. Trdnostni pogoj za tangencialne napetosti lahko zapišemo v obliki

Kje R s - konstrukcijska odpornost materiala nosilca na strig. Vrednote R s za osnovne gradbene materiale so podani v ustreznih oddelkih SNiP.

Strižne napetosti lahko dosežejo pomembne vrednosti v mrežah I-nosilcev, zlasti v tankih mrežah kompozitnih nosilcev.

Izračun strižne napetosti je lahko kritičen za lesene tramove, saj se les slabo upira drobljenju vzdolž vlakna. Tako je na primer za bor izračunana odpornost na napetost in stiskanje med upogibanjem R= 13 MPa in pri striženju vzdolž vlaken RCK= 2,4 MPa. Takšen izračun je potreben tudi pri ocenjevanju trdnosti veznih elementov sovprežnih nosilcev - zvarov, sornikov, zakovic, moznikov itd.

Pogoj za strižno trdnost vzdolž vlaken za leseni nosilec pravokotnega prereza ob upoštevanju formule (7.27) lahko zapišemo v obliki

Primer 7.15. Za žarek, prikazan na sl. 7,49, A, sestavimo diagrame Qy in M v Izberemo odsek žarka v obliki valjanega jeklenega I-žarka in narišemo diagrame c x in t v odsekih z največjim Qy in Mz. Varnostni faktor obremenitve y f = 1.2, konstrukcijska odpornost R= 210 MPa = 21 kN/cm 2, obratovalni pogoji koeficient y c = 1,0.

Izračun začnemo z določitvijo reakcij podpore:

Izračunajmo vrednosti Qy in M z v značilnih odsekih žarka.

Prečne sile znotraj vsakega odseka nosilca so konstantne vrednosti in imajo skoke v odsekih pod silo in na podpori IN. Upogibni momenti se spreminjajo linearno. Diagrami Qy in M z so prikazani na sl. 7,49, b, c.

Nevaren odsek je v sredini razpona nosilca, kjer je upogibni moment največji. Izračunajmo izračunano vrednost največjega upogibnega momenta:

Potreben moment upora je

Glede na sortiment sprejmemo odsek 127 in izpišemo potrebne geometrijske značilnosti odseka (sl. 7.50, A):

Izračunajmo vrednosti najvišjih normalnih napetosti v nevarnem delu žarka in preverimo njegovo trdnost:

Trdnost žarka je zagotovljena.

Tangencialne napetosti imajo največje vrednosti na odseku nosilca, kjer deluje največja absolutna velikost prečne sile (2 nb = 35 kN.

Projektna vrednost strižne sile

Izračunajmo vrednosti tangencialnih napetosti v steni I-nosilca na ravni nevtralne osi in na ravni vmesnika med steno in prirobnicami:

Diagrami c x in x, v odseku l: = 2,4 m (desno) sta prikazana na sl. 7.50, b, c.

Predznak tangencialnih napetosti je negativen, saj ustreza predznaku strižne sile.

Primer 7.16. Za leseni žarek pravokotnega prereza (slika 7.51, A) sestavimo diagrame Q in Mz, določite višino odseka h iz stanja moči, jemanje R = = 14 MPa, yy= 1,4 in y c = 1,0 in preverite trdnost žarka za striženje na nevtralni plasti, pri čemer RCK= 2,4 MPa.

Določimo reakcije podpore:

Izračunajmo vrednosti Q v in M z
v značilnih odsekih žarka.

Znotraj drugega odseka postane strižna sila enaka nič. Položaj tega odseka najdemo iz podobnosti trikotnikov na diagramu Q y:

Izračunajmo skrajno vrednost upogibnega momenta v tem delu:

Diagrami Qy in M z so prikazani na sl. 7.51, b, c.

Odsek nosilca, kjer se pojavi največji upogibni moment, je nevaren. Izračunajmo izračunano vrednost upogibnega momenta v tem delu:

Zahtevani modul preseka

S formulo (7.20) izrazimo uporni moment skozi višino preseka h in ga enačite z zahtevanim momentom upora:

Vzamemo pravokotni odsek 12x18 cm, izračunamo geometrijske značilnosti odseka:

Določimo najvišje normalne napetosti v nevarnem delu nosilca in preverimo njegovo trdnost:

Pogoj trdnosti je izpolnjen.

Za preverjanje strižne trdnosti nosilca vzdolž vlaken je treba določiti vrednosti največjih tangencialnih napetosti v odseku z največjo absolutno vrednostjo prečne sile 0 nb = 6 kN. Izračunana vrednost strižne sile v tem odseku

Največje strižne napetosti v prerezu delujejo v višini nevtralne osi. Po zakonu združevanja delujejo tudi v nevtralni plasti in težijo k temu, da povzročijo premik enega dela žarka glede na drugi del.

S formulo (7.27) izračunamo vrednost mmax in preverimo strižno trdnost žarka:

Pogoj strižne trdnosti je izpolnjen.

Primer 7.17. Za okrogel leseni žarek (slika 7.52, A) sestavimo diagrame Q y n M z n Iz pogoja trdnosti določimo zahtevani premer prereza. Pri izračunih bomo sprejeli R= 14 MPa, yy = 1,4 in y s = 1,0.

Določimo reakcije podpore:

Izračunajmo vrednosti Q in M 7 v značilnih odsekih žarka.

Diagrami Qy in M z so prikazani na sl. 7,52, b, c. Odsek o podpori je nevaren IN z največjim upogibnim momentom v absolutni vrednosti Mnb = 4 kNm. Izračunana vrednost upogibnega momenta v tem odseku

Izračunajmo zahtevani moment upora odseka:

S formulo (7.21) za moment upora krožnega prereza najdemo zahtevani premer:

Sprejmimo D= 16 cm in določi največje normalne napetosti v nosilcu:

Primer 7.18. Določimo nosilnost škatlastega nosilca 120x180x10 mm, obremenjenega po diagramu na sl. 7,53, A. Zgradimo diagrame c x itd. na nevarnem odseku. Material nosilca - jeklo razreda VStZ, R= 210 MPa = 21 kN/cm2, U/= U, Mi =°’ 9 -

Diagrami Qy in M z so prikazani na sl. 7,53, A.

Nevaren je odsek nosilca ob vgradnji, kjer je upogibni moment M nb absolutno največji. - P1 = 3,2 R.

Izračunajmo vztrajnostni in uporni moment škatlastega odseka:

Ob upoštevanju formule (7.37) in dobljene vrednosti za L/nb določimo izračunano vrednost sile R:

Normativna vrednost sile

Najvišje normalne napetosti v nosilcu zaradi konstrukcijske sile

Izračunajmo statični moment polovice odseka ^1/2 in statični moment površine prečnega prereza prirobnice S n glede na nevtralno os:

Tangencialne napetosti na ravni nevtralne osi in na ravni vmesnika prirobnica-stena (sl. 7.53, b) so enaki:

Diagrami Oh in t uh v prerezu blizu vgradnje so prikazani na sl. 7,53, v, g.

Začeli bomo z najpreprostejšim primerom, tako imenovanim čistim upogibom.

Čisti upogib je poseben primer upogiba, pri katerem je prečna sila v odsekih nosilca enaka nič. Do čistega upogibanja lahko pride le, če je lastna teža nosilca tako majhna, da je njen vpliv mogoče zanemariti. Za nosilce na dveh nosilcih primeri obremenitev, ki povzročajo čisto

upogibanje, prikazano na sl. 88. V odsekih teh žarkov, kjer je Q = 0 in zato M = const; pride do čistega upogibanja.

Sile v katerem koli odseku žarka med čistim upogibanjem se zmanjšajo na par sil, katerih ravnina delovanja poteka skozi os žarka, moment pa je konstanten.

Napetosti je mogoče določiti na podlagi naslednjih premislekov.

1. Tangencialne komponente sil vzdolž elementarnih območij v prerezu nosilca ni mogoče reducirati na par sil, katerih ravnina delovanja je pravokotna na ravnino prereza. Iz tega sledi, da je upogibna sila v prerezu posledica delovanja vzdolž elementarnih površin

samo normalne sile, zato se pri čistem upogibu napetosti zmanjšajo samo na normalne.

2. Da bi se prizadevanja na osnovnih mestih zmanjšala na samo nekaj sil, morajo biti med njimi tako pozitivne kot negativne. Zato morajo obstajati napetostna in kompresijska vlakna žarka.

3. Zaradi dejstva, da so sile v različnih odsekih enake, so napetosti na ustreznih točkah odsekov enake.

Razmislimo o nekem elementu blizu površine (slika 89, a). Ker vzdolž njegovega spodnjega roba, ki sovpada s površino nosilca, ne delujejo sile, na njem ni napetosti. Na zgornjem robu elementa torej ni nobenih napetosti, saj drugače element ne bi bil v ravnovesju.Upoštevajoč element, ki meji nanj po višini (slika 89, b), pridemo do

Isti zaključek, itd. Iz tega sledi, da vzdolž vodoravnih robov nobenega elementa ni napetosti. Ob upoštevanju elementov, ki tvorijo vodoravno plast, začenši z elementom blizu površine nosilca (slika 90), pridemo do zaključka, da vzdolž stranskih navpičnih robov nobenega elementa ni napetosti. Tako je treba napetostno stanje katerega koli elementa (sl. 91, a) in v meji vlaken predstaviti, kot je prikazano na sl. 91,b, kar pomeni, da gre lahko za osno napetost ali osno stiskanje.

4. Zaradi simetrije uporabe zunanjih sil mora odsek vzdolž sredine dolžine žarka po deformaciji ostati ravno in normalno na os žarka (slika 92, a). Iz istega razloga tudi odseki v četrtinah dolžine žarka ostanejo ravni in normalni na os žarka (slika 92, b), razen če skrajni odseki žarka med deformacijo ostanejo ravni in normalni na os žarka. žarek. Podoben zaključek velja za odseke v osminah dolžine žarka (slika 92, c) itd. Posledično, če med upogibanjem zunanji odseki žarka ostanejo ravni, potem za kateri koli odsek ostane

Poštena je izjava, da po deformaciji ostane ravna in normalna na os ukrivljenega nosilca. Toda v tem primeru je očitno, da se mora sprememba raztezka vlaken žarka vzdolž njegove višine zgoditi ne samo neprekinjeno, ampak tudi monotono. Če plast imenujemo niz vlaken, ki imajo enake raztezke, potem iz povedanega sledi, da morajo biti raztegnjena in stisnjena vlakna žarka nameščena na nasprotnih straneh plasti, v kateri so raztezki vlaken enaki na nič. Vlakna, katerih raztezki so nič, bomo imenovali nevtralna; plast, sestavljena iz nevtralnih vlaken, je nevtralna plast; črta presečišča nevtralne plasti z ravnino prečnega prereza žarka - nevtralna črta tega odseka. Nato je na podlagi prejšnjega sklepanja mogoče trditi, da je pri čistem upogibu žarka v vsakem odseku nevtralna črta, ki ta odsek deli na dva dela (coni): cono raztegnjenih vlaken (raztegnjena cona) in cona stisnjenih vlaken (stisnjena cona). ). V skladu s tem morajo na točkah raztegnjenega območja odseka delovati normalne natezne napetosti, na točkah stisnjenega območja - tlačne napetosti, na točkah nevtralne črte pa so napetosti enake nič.

Tako s čistim upogibanjem nosilca s konstantnim prerezom:

1) v odsekih delujejo samo normalne napetosti;

2) celoten odsek lahko razdelimo na dva dela (cone) - raztegnjen in stisnjen; meja območij je črta nevtralnega odseka, na točkah katere so normalne napetosti enake nič;

3) kateri koli vzdolžni element žarka (v meji katero koli vlakno) je izpostavljen aksialni napetosti ali stiskanju, tako da sosednja vlakna ne delujejo med seboj;

4) če skrajni odseki žarka med deformacijo ostanejo ravni in normalni na os, potem ostanejo vsi njegovi prerezi ravni in normalni na os ukrivljenega žarka.

Napetostno stanje nosilca pri čistem upogibu

Razmislimo o elementu žarka, ki je podvržen čistemu upogibanju, in zaključimo ki se nahaja med odseki m-m in n-n, ki sta drug od drugega oddaljena na neskončno majhni razdalji dx (slika 93). Zaradi položaja (4) prejšnjega odstavka bosta odseka m- m in n - n, ki sta bila pred deformacijo vzporedna, po upogibu ostala ravna, tvorila kot dQ in se sekala vzdolž premice, ki poteka skozi točko C, ki je središče ukrivljenosti nevtralno vlakno NN. Nato se med njima zaprti del AB vlakna, ki se nahaja na razdalji z od nevtralnega vlakna (pozitivna smer osi z je med upogibanjem vzeta proti konveksnosti nosilca), se po deformaciji spremeni v lok AB. kos nevtralnega vlakna O1O2, ki se spremeni v lok, O1O2 ne bo spremenil svoje dolžine, vlakno AB pa bo dobilo raztezek:

pred deformacijo

po deformaciji

kjer je p polmer ukrivljenosti nevtralnega vlakna.

Zato je absolutno podaljšanje segmenta AB enako

in relativni raztezek

Ker je v skladu s položajem (3) vlakno AB izpostavljeno aksialni napetosti, potem med elastično deformacijo

To kaže, da so normalne napetosti vzdolž višine nosilca porazdeljene po linearnem zakonu (slika 94). Ker mora biti enaka sila vseh sil na vseh elementarnih prerezih enaka nič, potem

od koder z zamenjavo vrednosti iz (5.8) najdemo

Toda zadnji integral je statični moment okoli osi Oy, pravokoten na ravnino delovanja upogibnih sil.

Zaradi svoje enakosti na nič mora ta os potekati skozi težišče O preseka. Tako je nevtralna črta odseka nosilca ravna črta y, pravokotna na ravnino delovanja upogibnih sil. Imenuje se nevtralna os odseka žarka. Potem iz (5.8) sledi, da so napetosti v točkah, ki ležijo na enaki razdalji od nevtralne osi, enake.

Primer čistega upogiba, pri katerem upogibne sile delujejo samo v eni ravnini in povzročajo upogib le v tej ravnini, je ravninski čisti upogib. Če omenjena ravnina poteka skozi os Oz, mora biti moment elementarnih sil glede na to os enak nič, tj.

Če tukaj zamenjamo vrednost σ iz (5.8), dobimo

Integral na levi strani te enakosti je, kot je znano, centrifugalni vztrajnostni moment preseka glede na osi y in z, torej

Osi, glede katerih je centrifugalni vztrajnostni moment odseka enak nič, se imenujejo glavne vztrajnostne osi tega odseka. Če poleg tega prehajajo skozi težišče odseka, jih lahko imenujemo glavne osrednje vztrajnostne osi odseka. Tako sta pri ravnem čistem upogibu smer ravnine delovanja upogibnih sil in nevtralna os preseka glavni osrednji vztrajnostni osi slednjega. Z drugimi besedami, da bi dobili ravno, čisto krivino žarka, obremenitve ni mogoče uporabiti poljubno: zmanjšati jo je treba na sile, ki delujejo v ravnini, ki poteka skozi eno od glavnih osrednjih vztrajnostnih osi odsekov nosilca. žarek; v tem primeru bo druga glavna osrednja vztrajnostna os nevtralna os preseka.

Kot je znano, je v primeru odseka, ki je simetričen glede na katero koli os, simetrijska os ena njegovih glavnih osrednjih vztrajnostnih osi. Posledično bomo v tem konkretnem primeru zagotovo dobili čisti upogib z uporabo ustreznih obremenitev v ravnini, ki poteka skozi vzdolžno os nosilca in simetrično os njegovega preseka. Ravna črta, ki je pravokotna na simetrično os in poteka skozi težišče odseka, je nevtralna os tega odseka.

Po določitvi položaja nevtralne osi ni težko najti velikosti napetosti na kateri koli točki preseka. Dejansko mora biti vsota momentov elementarnih sil glede na nevtralno os yy enaka upogibnemu momentu, potem

od koder nadomestimo vrednost σ iz (5.8), dobimo

Ker je integral je. vztrajnostni moment odseka glede na os yy, torej

in iz izraza (5.8) dobimo

Produkt EI Y se imenuje upogibna togost nosilca.

Največje natezne in največje tlačne napetosti v absolutni vrednosti delujejo v točkah preseka, za katere je absolutna vrednost z največja, to je v točkah, ki so najbolj oddaljene od nevtralne osi. Z oznako, sl. 95 imamo

Vrednost Jy/h1 se imenuje moment odpornosti preseka na napetost in je označena z Wyr; podobno se Jy/h2 imenuje moment upora preseka proti stiskanju

in označuje Wyc, torej

in zato

Če je nevtralna os simetrijska os preseka, potem je h1 = h2 = h/2 in zato Wyp = Wyc, zato ju ni treba razlikovati in uporabljata isti zapis:

W y imenujemo preprosto uporni moment odseka. Posledično v primeru odseka, ki je simetričen glede na nevtralno os,

Vsi zgornji zaključki so bili pridobljeni na podlagi predpostavke, da prečni prerezi nosilca, ko so upognjeni, ostanejo ravni in normalni na svojo os (hipoteza ravnih prerezov). Kot je bilo prikazano, ta predpostavka velja le v primeru, ko skrajni (končni) odseki nosilca med upogibanjem ostanejo ravni. Po drugi strani pa iz hipoteze ravninskih prerezov sledi, da bi morale biti elementarne sile v takih odsekih porazdeljene po linearnem zakonu. Zato je za veljavnost nastale teorije ravnega čistega upogiba potrebno, da se upogibni momenti na koncih nosilca uporabijo v obliki elementarnih sil, porazdeljenih po višini odseka po linearnem zakonu (sl. 96), ki sovpada z zakonom porazdelitve napetosti vzdolž višine prerezov. Vendar pa je na podlagi načela Saint-Venant mogoče trditi, da bo sprememba metode uporabe upogibnih momentov na koncih nosilca povzročila le lokalne deformacije, katerih učinek bo vplival le na določeno razdaljo od teh koncev (približno enako na višino odseka). Odseki, ki se nahajajo po preostali dolžini žarka, bodo ostali ravni. Posledično navedena teorija ravnega čistega upogiba za katero koli metodo uporabe upogibnih momentov velja samo v srednjem delu dolžine nosilca, ki se nahaja od njegovih koncev na razdaljah, ki so približno enake višini odseka. Od tu je jasno, da je ta teorija očitno neuporabna, če višina preseka presega polovico dolžine ali razpona nosilca.

Poglavje 1. KRIVLJENJE PRAVIH ČINIJSKIH NOSIL IN NOSILNIH SISTEMOV

1.1. Osnovne odvisnosti teorije upogiba nosilca

tramovi Običajno imenujemo palice, ki se upognejo pod vplivom prečne (normalne na os palice) obremenitve. Nosilci so najpogostejši elementi ladijskih konstrukcij. Os žarka je geometrijska lokacija težišč njegovih presekov v nedeformiranem stanju. Žarek se imenuje ravno, če je njegova os ravna črta. Geometrična lokacija težišč prerezov žarka v upognjenem stanju se imenuje elastična linija žarka. Sprejeta je naslednja smer koordinatnih osi: os OX poravnana z osjo žarka, in os ojoj in OZ– z glavnimi središčnimi vztrajnostnimi osmi prečnega prereza (slika 1.1).

Teorija upogibanja žarka temelji na naslednjih predpostavkah.

1. Sprejeta je hipoteza ravnih prerezov, po kateri prečni prerezi nosilca, sprva ravni in normalni na os nosilca, po upogibanju ostanejo ravni in normalni na elastično linijo nosilca. Zahvaljujoč temu se lahko upogibna deformacija nosilca obravnava neodvisno od strižne deformacije, ki povzroči izkrivljanje ravnin prečnega prereza nosilca in njihovo vrtenje glede na elastično linijo (slika 1.2, A).

2. Normalne napetosti v območjih, vzporednih z osjo žarka, so zanemarjene zaradi svoje majhnosti (slika 1.2, b).

3. Nosilci veljajo za dovolj toge, tj. njihovi odkloni so majhni v primerjavi z višino nosilcev, koti vrtenja odsekov pa so majhni v primerjavi z enoto (slika 1.2, V).

4. Napetosti in deformacije so povezane z linearno povezavo, tj. Velja Hookov zakon (slika 1.2, G).

riž. 1.2. Predpostavke teorije upogibanja žarka

Upoštevali bomo upogibne momente in strižne sile, ki se pojavijo pri upogibanju nosilca v njegovem prerezu kot posledica delovanja dela nosilca, ki je miselno vržen vzdolž prereza na njegov preostali del.

Moment vseh sil, ki delujejo v odseku glede na eno od glavnih osi, se imenuje upogibni moment. Upogibni moment je enak vsoti momentov vseh sil (vključno s podpornimi reakcijami in momenti), ki delujejo na zavrnjeni del nosilca glede na določeno os obravnavanega odseka.

Projekcija glavnega vektorja sil, ki delujejo v preseku, na presečno ravnino se imenuje strižna sila. Je enak vsoti projekcij na ravnino prečnega prereza vseh sil (vključno z reakcijami podpore), ki delujejo na zavrnjeni del nosilca..

Omejimo se na upoštevanje upogiba žarka, ki se pojavi v ravnini XOZ. Do takega upogibanja pride, ko bočna obremenitev deluje v ravnini, ki je vzporedna z ravnino XOZ, njegova rezultanta v vsakem odseku pa poteka skozi točko, imenovano središče upogiba odseka. Upoštevajte, da pri odsekih nosilcev, ki imajo dve simetrični osi, središče upogiba sovpada s težiščem, pri odsekih, ki imajo eno simetrijsko os, pa leži na simetrični osi, vendar ne sovpada s središčem gravitacija.

Obremenitev nosilcev, vključenih v trup ladje, je lahko porazdeljena (najpogosteje enakomerno porazdeljena vzdolž osi žarka ali spreminjajoča se po linearnem zakonu) ali uporabljena v obliki koncentriranih sil in momentov.

Intenzivnost porazdeljene obremenitve (obremenitev na enoto dolžine osi nosilca) označimo z q(x), zunanja koncentrirana sila – as R, zunanji upogibni moment pa je enak M. Porazdeljena obremenitev in koncentrirana sila sta pozitivni, če smeri njunega delovanja sovpadata s pozitivno smerjo osi. OZ(slika 1.3, A,b). Zunanji upogibni moment je pozitiven, če je usmerjen v smeri urinega kazalca (slika 1.3, V).

riž. 1.3. Pravilo znaka za zunanje obremenitve

Označimo odklon ravnega nosilca, ko je upognjen v ravnini XOZ skozi w, in kot zasuka odseka je skozi θ. Sprejmimo pravilo znakov za upogibne elemente (slika 1.4):

1) odklon je pozitiven, če sovpada s pozitivno smerjo osi OZ(slika 1.4, A):

2) kot vrtenja odseka je pozitiven, če se zaradi upogibanja odsek vrti v smeri urinega kazalca (sl. 1.4, b);

3) upogibni momenti so pozitivni, če se žarek pod njihovim vplivom upogne konveksno navzgor (sl. 1.4, V);

4) strižne sile so pozitivne, če vrtijo izbrani element žarka v nasprotni smeri urinega kazalca (slika 1.4, G).

riž. 1.4. Pravilo znaka za upogibne elemente

Na podlagi hipoteze ravnih odsekov je razvidno (slika 1.5), da je relativni raztezek vlakna ε x, ločeno z z od nevtralne osi bo enaka

ε x= −z/ρ ,(1.1)

Kje ρ – polmer ukrivljenosti žarka v obravnavanem odseku.

riž. 1.5. Diagram upogibanja žarka

Nevtralna os prečnega prereza je geometrijsko mesto točk, za katere je linearna deformacija med upogibanjem enaka nič. Med ukrivljenostjo in izpeljankami w(x) obstaja odvisnost

Zaradi sprejete predpostavke, da so vrtilni koti majhni za dovolj toge nosilce, je vrednostmajhna v primerjavi z enotnostjo, zato lahko domnevamo, da

Zamenjava 1/ ρ iz (1.2) v (1.1), dobimo

Normalna upogibna napetost σ x na podlagi Hookejevega zakona bo enako

Ker iz definicije nosilcev izhaja, da ni vzdolžne sile, usmerjene vzdolž osi nosilca, mora glavni vektor normalnih napetosti izginiti, tj.

Kje F– površina prečnega prereza nosilca.

Iz (1.5) dobimo, da je statični moment površine prečnega prereza nosilca enak nič. To pomeni, da gre nevtralna os preseka skozi njegovo težišče.

Moment notranjih sil, ki delujejo v prerezu glede na nevtralno os, moj volja

Če upoštevamo, da je vztrajnostni moment površine prečnega prereza glede na nevtralno os ojoj je enak in to vrednost nadomestimo v (1.6), dobimo odvisnost, ki izraža osnovno diferencialno enačbo za upogibanje nosilca

Moment notranjih sil v preseku glede na os OZ volja

Od osi ojoj in OZ po stanju so glavne središčne osi preseka, torej .

Iz tega sledi, da ko se obremenitev uporablja v ravnini, ki je vzporedna z glavno upogibno ravnino, bo elastična linija nosilca ravna krivulja. Ta ovinek se imenuje stanovanje. Na podlagi odvisnosti (1.4) in (1.7) dobimo

Formula (1.8) kaže, da so normalne napetosti med upogibanjem žarkov sorazmerne z razdaljo od nevtralne osi žarka. Seveda to izhaja iz hipoteze ravninskih prerezov. V praktičnih izračunih se za določitev najvišjih normalnih napetosti pogosto uporablja moment upora odseka nosilca

kjer | z| max – absolutna vrednost oddaljenosti najbolj oddaljenega vlakna od nevtralne osi.

V nadaljevanju indeksi l izpuščeno zaradi enostavnosti.

Med upogibnim momentom, strižno silo in intenzivnostjo prečne obremenitve obstaja povezava, ki izhaja iz ravnotežnega stanja elementa, ki je mentalno izoliran od nosilca.

Razmislite o elementu žarka z dolžino dx (slika 1.6). Pri tem se predpostavlja, da so deformacije elementa zanemarljive.

Če trenutek deluje v levem delu elementa M in rezalna sila n, potem bodo imele ustrezne sile v njegovem desnem delu prirastke. Upoštevajmo samo linearne prirastke .

Slika 1.6. Sile, ki delujejo na nosilni element

Izenačenje projekcije na os na nič OZ vseh sil, ki delujejo na element, in moment vseh sil glede na nevtralno os desnega odseka dobimo:

Iz teh enačb, natančnih na količine višjega reda majhnosti, dobimo

Iz (1.11) in (1.12) sledi, da

Odvisnosti (1.11)–(1.13) so znane kot Zhuravsky–Schwedlerjev izrek.Iz teh odvisnosti sledi, da lahko strižno silo in upogibni moment določimo z integracijo obremenitve q:

Kje n 0 in M 0 – strižna sila in upogibni moment v odseku, ki ustrezax =x 0 , ki je vzeta za izhodišče; ξ,ξ 1 – integracijske spremenljivke.

Trajna n 0 in M 0 za statično določene nosilce lahko določimo iz pogojev njihovega statičnega ravnovesja.

Če je nosilec statično določen, lahko upogibni moment na katerem koli prerezu najdemo z uporabo (1.14), elastično linijo pa določimo z dvakratno integracijo diferencialne enačbe (1.7). Statično določljivi nosilci pa so izjemno redki v konstrukcijah ladijskega trupa. Večina nosilcev, ki sestavljajo ladijske strukture, tvori več statično nedoločenih sistemov. V teh primerih je enačba (1.7) neprimerna za določanje elastične črte, zato je priporočljivo preiti na enačbo četrtega reda.

1.2. Diferencialna enačba za upogibne nosilce

Diferencialna enačba (1.7) za splošni primer, ko je vztrajnostni moment preseka funkcija x, ob upoštevanju (1.11) in (1.12) dobimo:

kjer praštevila označujejo razlikovanje glede na x.

Za prizmatične nosilce, tj. nosilcev s konstantnim prerezom, dobimo naslednje diferencialne upogibne enačbe:

Navadno nehomogeno linearno diferencialno enačbo četrtega reda (1.18) lahko predstavimo kot niz štirih diferencialnih enačb prvega reda:

Za določitev upogiba nosilca (njegove elastične črte) in vseh neznanih upogibnih elementov uporabimo naslednjo enačbo (1.18) ali sistem enačb (1.19): w(x), θ (x), M(x), n(x).

Integracija (1.18) 4-krat zaporedno (ob predpostavki, da levi konec žarka ustreza odsekux= xa ), dobimo:

Preprosto je videti, da so integracijske konstante ne,Ma,θ a , w a imajo določen fizični pomen, in sicer:

N a– strižna sila na začetku štetja, tj. pri x =xa ;

M a– upogibni moment na začetku referenčne točke;

θ a – kot zasuka na začetku štetja;

w a – upogibanje v istem delu.

Če želite določiti te konstante, lahko vedno ustvarite štiri robne pogoje - dva za vsak konec nosilca z enim razponom. Seveda so robni pogoji odvisni od razporeditve koncev nosilca. Najenostavnejši pogoji ustrezajo zgibni podpori na togih nosilcih ali togi vgradnji.

Ko je konec nosilca tečajno podprt na togi nosilec (slika 1.7, A) odklon žarka in upogibni moment sta nič:

S togo vgradnjo na togi nosilec (slika 1.7, b) odklon in kot zasuka odseka sta enaka nič:

Če je konec nosilca (konzola) prost (slika 1.7, V), potem sta v tem delu upogibni moment in strižna sila enaka nič:

Možna situacija je povezana z drsečo vgradnjo ali vgradnjo simetrije (slika 1.7, G). To vodi do naslednjih robnih pogojev:

Upoštevajte, da se robni pogoji (1.26), ki se nanašajo na odklone in rotacijske kote, običajno imenujejo kinematična, in pogoji (1.27) – s silo.

riž. 1.7. Vrste robnih pogojev

Pri ladijskih konstrukcijah imamo pogosto opravka s kompleksnejšimi robnimi pogoji, ki ustrezajo naslonjanju nosilca na elastične nosilce ali elastične zaključke koncev.

Elastična podpora (slika 1.8, A) je podpora, ki ima znižanje sorazmerno z reakcijo, ki deluje na podlago. Upoštevali bomo reakcijo elastične podpore R pozitivno, če deluje na nosilec v smeri pozitivne smeri osi OZ. Potem lahko zapišemo:

w =AR,(1.29)

Kje A– sorazmernostni koeficient, imenovan koeficient podajnosti elastične podpore.

Ta koeficient je enak posedanju elastičnega nosilca pod delovanjem reakcije R= 1, tj. A=w R = 1 .

Elastične podpore v konstrukcijah ladij so lahko nosilci, ki ojačajo zadevni nosilec, ali stebri in druge konstrukcije, ki delujejo na stiskanje.

Za določitev koeficienta podajnosti elastične podpore A potrebno je obremeniti ustrezno konstrukcijo z enoto sile in poiskati absolutno vrednost posedanja (upogiba) na točki delovanja sile. Toga podpora je poseben primer elastične podpore z A= 0.

Elastično tesnjenje (slika 1.8, b) je nosilna konstrukcija, ki preprečuje prosto vrtenje preseka in pri kateri je vrtilni kot θ v tem preseku sorazmeren momentu, tj. obstaja odvisnost

θ = Â M.(1.30)

Proporcionalni množitelj  se imenuje koeficient elastične vgradnje in ga je mogoče opredeliti kot kot zasuka elastične vgradnje pri M = 1, tj.  = θ M = 1 .

Poseben primer elastičnega tesnjenja z  = 0 je trda prekinitev. V ladijskih konstrukcijah so elastične vgradnje običajno nosilci, normalni na obravnavanega in ležeči v isti ravnini. Na primer, tramovi itd. se lahko štejejo za elastično vdelane v okvirje.

riž. 1.8. Elastična opora ( A) in elastično tesnilo ( b)

Če so konci žarka dolgi L so podprte na elastičnih nosilcih (slika 1.9), potem so reakcije nosilcev v končnih odsekih enake strižnim silam, robne pogoje pa lahko zapišemo:

Predznak minus v prvem pogoju (1.31) je sprejet, ker pozitivna strižna sila v levem nosilnem odseku ustreza reakciji, ki deluje na nosilec od zgoraj navzdol in na nosilec od spodaj navzgor.

Če so konci žarka dolgi Lelastično zatesnjena(Sl. 1.9), nato pa za podporne odseke, ob upoštevanju pravila znakov za kote vrtenja in upogibne momente, lahko zapišemo:

Predznak minus v drugem pogoju (1.32) je sprejet, ker je s pozitivnim momentom v desnem nosilnem delu nosilca moment, ki deluje na elastično tesnilo, usmerjen v nasprotni smeri urinega kazalca, pozitivni kot vrtenja v tem delu pa je usmerjen v smeri urinega kazalca, tj. smeri momenta in kota vrtenja ne sovpadata.

Upoštevanje diferencialne enačbe (1.18) in vseh robnih pogojev pokaže, da so linearni tako glede na upogibe, ki so vanje vključeni, kot tudi glede na njihove odvode ter obremenitve, ki delujejo na nosilec. Linearnost je posledica predpostavk o veljavnosti Hookovega zakona in majhnosti odklonov žarka.

riž. 1.9. Nosilec, katerega oba konca sta elastično podprta in elastično vpeta ( A);

sile v elastičnih nosilcih in elastičnih tesnilih, ki ustrezajo pozitivnim
smeri upogibnega momenta in strižne sile ( b)

Kadar na nosilec deluje več obremenitev, je vsak upogibni element nosilca (upogib, kot zasuka, moment in strižna sila) vsota upogibnih elementov zaradi delovanja vsake obremenitve posebej. To zelo pomembno stališče, imenovano načelo superpozicije ali načelo seštevanja delovanja obremenitev, se pogosto uporablja v praktičnih izračunih in zlasti za razkrivanje statične nedoločenosti nosilcev.

1.3. Metoda začetnih parametrov

Splošni integral diferencialne enačbe za upogibanje nosilca lahko uporabimo za določitev elastične črte enorazponskega nosilca v primeru, ko je obremenitev nosilca zvezna funkcija koordinate v celotnem razponu. Če obremenitev vsebuje koncentrirane sile, momente ali porazdeljena obremenitev deluje na del dolžine nosilca (slika 1.10), potem izraza (1.24) ni mogoče uporabiti neposredno. V tem primeru bi bilo mogoče določiti elastične črte v odsekih 1, 2 in 3 skozi w 1 , w 2 , w 3, zapišite integral za vsakega od njih v obliki (1.24) in poiščite vse poljubne konstante iz robnih pogojev na koncih žarka in pogojev konjugacije na mejah odsekov. Pogoji združevanja v obravnavanem primeru so izraženi na naslednji način:

pri x=a 1

pri x=a 2

pri x=a 3

Lahko vidimo, da ta način reševanja problema vodi do velikega števila poljubnih konstant, enakih 4 n, Kje n– število odsekov vzdolž dolžine žarka.

riž. 1.10. Žarek, v ločenih delih katerega se uporabljajo obremenitve različnih vrst

Veliko bolj priročno je prikazati elastično linijo žarka v obliki

kjer se upoštevajo izrazi onkraj dvojne črte, ko x³ a 1, x³ a 2 itd.

Očitno je, da je δ 1 w(x)=w 2 (x)−w 1 (x); δ2 w(x)=w 3 (x)−w 2 (x); itd.

Diferencialne enačbe za določanje popravkov elastične premice δ jazw (x) na podlagi (1.18) in (1.32) lahko zapišemo v obliki

Splošni integral za vsak popravek δ jazw (x) na elastično črto lahko zapišemo v obliki (1.24) z xa = a i . V tem primeru parametri ne,Ma,θ a , w a imajo pomen sprememb (skokov): v strižni sili, upogibnem momentu, kotu zasuka in odklonski puščici pri prehodu skozi odsek x =a i . Ta tehnika se imenuje metoda začetnih parametrov. Lahko se pokaže, da je za žarek, prikazan na sl. 1.10, bo enačba elastične črte

Metoda začetnih parametrov torej omogoča, da tudi v primeru diskontinuitete obremenitev zapišemo enačbo elastične črte v obliki, ki vsebuje samo štiri poljubne konstante. n 0 , M 0 , θ 0 , w 0, ki so določene iz robnih pogojev na koncih nosilca.

Upoštevajte, da so bile za veliko število variant enojnih nosilcev, ki se pojavljajo v praksi, sestavljene podrobne upogibne tabele, ki olajšajo iskanje upogibov, kotov vrtenja in drugih upogibnih elementov.

1.4. Določanje strižnih napetosti pri upogibu nosilcev

Hipoteza ravnih odsekov, sprejeta v teoriji upogibanja nosilca, vodi do dejstva, da je strižna deformacija v odseku nosilca enaka nič in s Hookeovim zakonom ne moremo določiti strižnih napetosti. Ker pa v splošnem primeru strižne sile delujejo v odsekih nosilca, bi morale nastati ustrezne tangencialne napetosti. Temu protislovju (ki je posledica sprejete hipoteze o ravninskih prerezih) se lahko izognemo z upoštevanjem ravnotežnih pogojev. Predpostavimo, da so pri upogibanju nosilca, sestavljenega iz tankih trakov, tangencialne napetosti v prerezu vsakega od teh trakov enakomerno porazdeljene po debelini in usmerjene vzporedno z dolgimi stranicami njegove konture. To stališče je praktično potrjeno z natančnimi rešitvami teorije elastičnosti. Razmislimo o žarku odprtega tankostenskega I-žarka. Na sl. Slika 1.11 prikazuje pozitivno smer tangencialnih napetosti v prirobnicah in steni profila med upogibanjem v ravnini stene nosilca. Poudarimo z vzdolžnim prerezom JAZ -jaz in dva prečna prereza dolžine elementa dx (slika 1.12).

Tangencialno napetost v navedenem vzdolžnem prerezu označimo z τ, normalne sile v začetnem prerezu pa z T. Normalne sile v končnem odseku bodo imele prirastke. Upoštevajmo torej samo linearne prirastke.

riž. 1.12. Vzdolžne sile in strižne napetosti
v elementu prirobnice nosilca

Pogoj statičnega ravnovesja elementa, izbranega iz nosilca (projekcije sil na os so enake nič OX) volja

Kje ; f– območje dela profila, odrezano s črto JAZ -jaz; δ – debelina profila na prerezu.

Iz (1.36) sledi:

Ker normalne napetosti σ x so določene s formulo (1.8), potem

V tem primeru predpostavimo, da ima žarek po svoji dolžini konstanten presek. Statični moment dela profila (odrezan po črti JAZ -jaz) glede na nevtralno os odseka nosilca ojoj je integral

Nato iz (1.37) za absolutno vrednost napetosti dobimo:

Seveda dobljena formula za določanje strižnih napetosti velja tudi za kateri koli vzdolžni prerez, npr. II –II(glej sliko 1.11) in statični moment S ots se izračuna za odrezani del območja profila žarka glede na nevtralno os brez upoštevanja predznaka.

Formula (1.38) v smislu izpeljave določa tangencialne napetosti v vzdolžnih prerezih nosilca. Iz izreka o parjenju tangencialnih napetosti, znanega iz tečaja o trdnosti materialov, sledi, da enake tangencialne napetosti delujejo na ustreznih točkah prečnega prereza nosilca. Seveda je projekcija glavnega vektorja tangencialnih napetosti na os OZ mora biti enak strižni sili n v določenem delu žarka. Ker so v nosilcih žarkov te vrste, kot je prikazano na sl. 1.11 so tangencialne napetosti usmerjene vzdolž osi ojoj, tj. normalni na ravnino delovanja obremenitve in so na splošno uravnoteženi, mora biti strižna sila uravnotežena s strižnimi napetostmi v nosilcu. Porazdelitev tangencialnih napetosti po višini stene sledi zakonu spremembe statičnega momenta S odrezanega dela območja glede na nevtralno os (pri konstantni debelini stene δ).

Razmislimo o simetričnem odseku I-žarka s prirobnico F 1 in območje stene ω = hδ (slika 1.13).

riž. 1.13. Odsek I-žarka

Statični moment odrezanega dela območja za točko, ki se nahaja na z od nevtralne osi bo

Kot je razvidno iz odvisnosti (1.39), se statični moment spreminja z z po zakonu kvadratne parabole. Najvišja vrednost S ots in s tem tangencialne napetosti τ , dobimo na nevtralni osi, kjer z = 0:

Največja strižna napetost v steni nosilca na nevtralni osi

Ker je vztrajnostni moment zadevnega odseka žarka enak

potem bo največja strižna napetost

Odnos n/ω ni nič drugega kot povprečna strižna napetost v steni, izračunana ob predpostavki enakomerne porazdelitve napetosti. Vzemimo za primer ω = 2 F 1 , po formuli (1.41) dobimo

Tako ima obravnavani nosilec največjo tangencialno napetost v steni na nevtralni osi le za 12,5 %. presega povprečno vrednost teh napetosti. Treba je opozoriti, da za večino profilov nosilcev, ki se uporabljajo v ladijskih trupih, največje strižne napetosti presegajo povprečne za 10–15%.

Če upoštevamo porazdelitev strižnih napetosti med upogibanjem v odseku nosilca, prikazanem na sl. 1.14, potem lahko vidite, da tvorijo moment glede na težišče odseka. V splošnem primeru upogibanje takega žarka v ravnini XOZ bo spremljalo zvijanje.

Upogibanje žarka ne spremlja zvijanje, če obremenitev deluje v ravnini, ki je vzporedna z XOZ ki poteka skozi točko, imenovano središče ovinka. Za to točko je značilno, da je moment vseh tangencialnih sil v odseku žarka glede na to enak nič.

riž. 1.14. Tangencialne napetosti med upogibanjem nosilca kanala (točka A – središče ovinka)

Oznaka razdalje središča ovinka A od osi nosilne stene skozi e, zapišemo pogoj, da je moment tangencialnih sil glede na točko enak nič A:

Kje Q 2 – tangencialna sila v zidu, enaka prečni sili, t.j. Q 2 =n;

Q 1 =Q 3 – sila v pasu, določena na podlagi (1.38) z odvisnostjo

Strižna deformacija (ali strižni kot) γ se spreminja vzdolž višine stene nosilca na enak način kot strižne napetosti τ , doseže največjo vrednost na nevtralni osi.

Kot je bilo prikazano, je pri nosilcih s tetivami sprememba tangencialnih napetosti vzdolž višine stene zelo nepomembna. To nam omogoča nadaljnje upoštevanje določenega povprečnega strižnega kota v steni nosilca

Strižna deformacija vodi do dejstva, da se pravi kot med ravnino prečnega prereza nosilca in tangento na elastično črto spremeni za količino γ Sre Poenostavljen diagram strižne deformacije nosilnega elementa je prikazan na sl. 1.15.

riž. 1.15. Diagram strižne deformacije nosilnega elementa

Po nakazani puščici upogiba, ki ga povzroči prerez w sdv, lahko zapišemo:

Upoštevanje pravila znakov za rezalno silo n in poiščite kot vrtenja

Zaradi ,

Z integracijo (1.47) dobimo

Konstanta a, vključeno v (1.48), določa premik žarka kot togega telesa in ga je mogoče vzeti enako kateri koli vrednosti, saj pri določanju skupne puščice odklona od upogibanja w upogibanje in striženje w SDV

pojavila se bo vsota integracijskih konstant w 0 +a, določeno iz robnih pogojev. Tukaj w 0 – odklon od upogiba v izhodišču.

Postavimo v prihodnost a=0. Potem bo končni izraz za elastično linijo, ki jo povzroča strig, dobil obliko

Upogibne in strižne komponente elastične linije so prikazane na sl. 1.16.

riž. 1.16. Bend ( A) in striženje ( b) komponente elastične črte nosilca

V obravnavanem primeru je kot zasuka odsekov med strigom enak nič, zato so ob upoštevanju striga koti zasuka odsekov, upogibni momenti in strižne sile povezani le z odpeljankami elastične črte iz bend:

Nekoliko drugačna je situacija pri koncentriranih momentih, ki delujejo na nosilec, ki, kot bo prikazano v nadaljevanju, ne povzročajo upogibov zaradi striga, temveč vodijo le v dodatno rotacijo odsekov nosilca.

Razmislimo o nosilcu, ki je prosto podprt na togih nosilcih, v levem delu katerega trenutek velja M. Strižna sila bo v tem primeru stalna in enaka

Za desni referenčni odsek dobimo oz

.(1.52)

Izraza (1.51) in (1.52) lahko prepišemo kot

Izrazi v oklepajih označujejo relativni dodatek k kotu zasuka preseka, ki ga povzroči strig.

Če upoštevamo na primer preprosto podprto gredo, obremenjeno sredi svojega razpona s silo R(Sl. 1.18), potem bo odklon žarka pod silo enak

Upogibni upogib je mogoče ugotoviti iz tabel za upogibanje žarkov. Strižni upogib je določen s formulo (1.50), ob upoštevanju dejstva, da .

riž. 1.18. Diagram preprosto podprtega nosilca, obremenjenega s koncentrirano silo

Kot je razvidno iz formule (1.55), ima relativni dodatek k odklonu žarka zaradi striga enako strukturo kot relativni dodatek k kotu vrtenja, vendar z drugačnim numeričnim koeficientom.

Uvedemo notacijo

kjer je β numerični koeficient, odvisen od konkretne obravnavane naloge, zasnove nosilcev in obremenitve žarka.

Analizirajmo odvisnost koeficienta k od različnih dejavnikov.

Če upoštevamo, da dobimo namesto (1.56)

Vztrajnostni moment odseka žarka je vedno mogoče predstaviti v obliki

,(1.58)

kjer je α numerični koeficient, odvisen od oblike in značilnosti prereza. Tako je za I-žarek v skladu s formulo (1.40) z ω =2 F 1 bomo našli jaz = ωh 2/3, tj. α =1/3.

Upoštevajte, da se bo koeficient α povečal s povečanjem velikosti prirobnic nosilca.

Ob upoštevanju (1.58) lahko namesto (1.57) zapišemo:

Tako je vrednost koeficienta k bistveno odvisna od razmerja med razponom nosilca in njegovo višino, od oblike prereza (skozi koeficient α), razporeditve nosilcev in obremenitve nosilca (skozi koeficient β). Relativno daljši žarek ( h/L majhen), manjši je vpliv strižne deformacije. Za valjane profilne nosilce, povezane h/L manj kot 1/10÷1/8, korekcije premika praktično ni mogoče upoštevati.

Vendar pa je za nosilce s širokimi prirobnicami, kot so na primer kobilice, vrvice in flore v sestavi spodnjih etaž, vpliv striga in pri navedenih h/L se lahko izkaže za pomembno.

Opozoriti je treba, da strižne deformacije ne vplivajo le na povečanje upogibov nosilcev, temveč v nekaterih primerih tudi na rezultate razkrivanja statične nedoločenosti nosilcev in nosilnih sistemov.