द्विघात समीकरण को हल करने के गैर-मानक तरीके। सूत्र का उपयोग करके द्विघात समीकरण को हल करना। दो अलग हैं

म्युनिसिपल शैक्षिक संस्था

शेन्टालिंस्की नगरपालिका जिले के शेन्टालिंस्काया माध्यमिक विद्यालय नंबर 1 "शैक्षिक केंद्र" समारा क्षेत्र

स्वीकृत: सहमत: समीक्षित:

स्कूल निदेशक डिप्टी एम/ओ शिक्षकों की बैठक में ओआईए के निदेशक

गणित और भौतिकी

/ I. P. Almendeeva // G. P. Efremova / प्रोटोकॉल नं।

2010 से

एम / ओ . के प्रमुख

कक्षा 11 के लिए बीजगणित पाठ

स्टेपानोवा वेलेंटीना याकोवलेना

शेन्टाला 2010

व्याख्यात्मक नोट

शैक्षिक नीति का रणनीतिक उद्देश्य एक छात्र के व्यक्तित्व को विकसित करना और उसकी गतिविधि को प्रोत्साहित करना है, उच्च विद्यालय के छात्रों को उनके व्यावसायिक हितों और सतत शिक्षा के संबंध में इरादों के अनुसार पढ़ाने के लिए परिस्थितियों का निर्माण करना है। प्रस्तावित शैक्षणिक अनुभव की प्रासंगिकता शिक्षा की सामग्री का विस्तार करके पूर्व-पेशेवर प्रशिक्षण की समस्या को हल करने से जुड़ी है।

यूनिफाइड स्टेट परीक्षा के सीआईएम में पेश किए गए समीकरण और असमानताएं कठिनाइयों का कारण बनती हैं, हालांकि "समीकरण और असमानताएं" विषय का अध्ययन। समीकरणों और असमानताओं की प्रणाली "भौतिक और गणितीय प्रोफ़ाइल की 11 वीं कक्षा में 33 घंटे दिए गए हैं। इस स्थिति को बहुत व्यापक प्रकार के समीकरणों और अधिक द्वारा समझाया गया है। बड़ी मात्राउन्हें हल करने के तरीके, छात्रों का अपर्याप्त सैद्धांतिक प्रशिक्षण और पाठ में गैर-मानक समस्याओं को हल करने के लिए समर्पित समय की एक छोटी राशि।

इस पाठ्यक्रम की सामग्री

आपको कुछ अनुभागों को गहराई से देखने का अवसर देता है, हल करने के नए तरीके पेश करता है गणितीय ज्ञान और कौशल के सुधार और विकास में योगदान देता है, विषय में रुचि के निर्माण में योगदान देता है, गणित की भूमिका की समझ मानवीय गतिविधियाँ, समीकरणों, असमानताओं और प्रणालियों को हल करने से छात्रों के लिए बड़ी संख्या में अनुमानी तकनीकें खुलती हैं आमके लिए मूल्यवान गणितीय विकासव्यक्तित्व अनुसंधान और किसी अन्य गणितीय सामग्री पर उपयोग किया जाता है।

कार्यक्रम 34 घंटे के कक्षा निर्देश के लिए डिज़ाइन किया गया है और पूरे स्कूल वर्ष में चलता है।

कार्यक्रम के लेखक-संकलक यू.वी. लेपेखिना«« कार्य समीकरणों में मदद करते हैं।"

पाठ्यक्रम का उद्देश्य:

गणितीय ज्ञान और समीकरणों को हल करने से जुड़े कौशल की प्रणाली के छात्रों द्वारा एक स्थायी जागरूक महारत के लिए परिस्थितियों का निर्माण, रचनात्मक और अनुसंधान गतिविधियों के साथ छात्रों को परिचित करना;

बौद्धिक और संचार के विकास को बढ़ावा देना सामान्य सामाजिक अभिविन्यास के लिए आवश्यक गुण।

शैक्षिक गतिविधियों की प्रक्रिया में छात्रों के आत्म-साक्षात्कार के लिए परिस्थितियों का निर्माण।

पाठ्यक्रम के उद्देश्य: -

तर्कसंगत समीकरणों की अवधारणा से संबंधित सैद्धांतिक ज्ञान का व्यवस्थितकरण और सामान्यीकरण;

विभिन्न समीकरणों को हल करने के लिए छात्रों के बीच आवश्यक व्यावहारिक कौशल और क्षमताओं का निर्माण;

सामूहिक संज्ञानात्मक श्रम, तार्किक और रचनात्मक सोच के कौशल का विकास;

अनुसंधान कौशल का विकास।

शैक्षिक संभावनाओं के संदर्भ में छात्र को उसकी क्षमता का आकलन करने में मदद करें, छात्रों को एकीकृत राज्य परीक्षा के लिए तैयार करें।

सैद्धांतिक भाग में वैकल्पिक पाठ्यक्रम कार्यक्रम की सामग्री में गैर-मानक समस्याओं को हल करने के लिए एक एल्गोरिथ्म का अध्ययन, एक गणना सूत्र शामिल है। व्यावहारिक सामग्री में छात्रों के प्रशिक्षण के स्तर को ध्यान में रखते हुए जटिलता के विभिन्न स्तरों के कार्य शामिल हैं।

इस कार्यक्रम का उद्देश्य पहले से ही महारत हासिल कौशल में और सुधार करना है, गहन ज्ञान के निर्माण में, ज्ञान के आवेदन को आसपास की वास्तविकता में देखने की क्षमता, गतिविधि की प्रक्रिया और सामग्री में छात्रों की एक स्थिर रुचि बनाती है, जैसा कि साथ ही संज्ञानात्मक और सामाजिक गतिविधि।

इस कार्यक्रम को लागू करने की प्रक्रिया में, जैसे शिक्षण विधियों:

समस्या सीखने की विधि, जिसकी मदद से छात्र वैज्ञानिक सोच के मानक प्राप्त करते हैं;

आंशिक खोज गतिविधि की विधि, समस्या के स्वतंत्र समाधान में योगदान;

एक शोध पद्धति जो स्कूली बच्चों को गैर-मानक सामग्री की समस्याओं को हल करने के तरीकों में महारत हासिल करने में मदद करेगी।

मूल रूपशैक्षिक प्रक्रिया का संगठन एक कहानी, बातचीत, संगोष्ठी, पाठ - कार्यशाला है , व्यक्तिगत कार्य विश्लेषण तैयार समाधान ... पाठ का एक हिस्सा कंप्यूटर (ग्राफिंग) पर काम करने के लिए समर्पित है। इसके अलावा, कुछ विषयों पर काम करते समय, स्वतंत्र कार्य और परीक्षण किए जाते हैं।

अनुमानित परिणाम:

छात्रों को पता होना चाहिए कि एक समीकरण क्या है, एक समीकरण की जड़, समकक्ष समीकरण और असमानताएं, समीकरण - परिणाम, बाहरी मूल, समीकरण की खोई हुई जड़; समीकरणों और असमानताओं को प्रकार से हल करने में सक्षम हो और प्रस्तावित विधियों द्वारा उन्हें हल कर सकें, यदि समान समीकरण को हल करना संभव हो विभिन्न तरीके, अधिक तर्कसंगत समाधान चुनें। अधिक जटिल समस्याओं को हल करने के लिए सीखे गए एल्गोरिदम को लागू करें

पाठ्यक्रम सामग्री

परिचय (1 एच)।

एक समीकरण की परिभाषा पर विचार करें, एक समीकरण की जड़, समकक्ष समीकरणों की परिभाषा, प्रमेय जिनकी सहायता से हम समकक्ष समीकरणों को पास करते हैं, उदाहरण जब एक समीकरण से दूसरे समीकरण में जाते समय, एक मूल खो जाता है या एक बाहरी जड़ दिखाई पड़ना।

संपूर्ण परिमेय समीकरण (12 घंटे)।

बीजीय समीकरणों का परिवर्तन। चयन विधि द्वारा बीजीय समीकरणों को हल करना। बीजगणितीय समीकरणों को समूहन और गुणन द्वारा हल करना। परिवर्तनीय विधि के परिवर्तन द्वारा बीजीय समीकरणों को हल करना। सजातीय समीकरण। एक पैरामीटर को पेश करने की विधि द्वारा बीजीय समीकरणों को हल करना। उलटा समीकरण .. अपरिभाषित गुणांक की विधि।

3. भिन्नात्मक परिमेय समीकरण। (8 घंटे)

सामान्य प्रावधान। एक परिमेय समीकरण को एक बीजीय समीकरण में घटाना। गुणनखंडन द्वारा परिमेय समीकरणों को हल करना और x . से विभाजित करना 0. चरों को बदलकर परिमेय समीकरणों को हल करना4. समीकरणों को हल करते समय कार्यों के गुणों का अनुप्रयोग (12 घंटे)

समीकरण को हल करते समय किसी फ़ंक्शन के डोमेन का उपयोग करना। समीकरणों को हल करते समय किसी फ़ंक्शन की एकरसता का उपयोग करना। समीकरण या असमानता के बाएँ और दाएँ पक्षों के रेखांकन करके समस्याओं को हल करना और चित्र से आवश्यक जानकारी को "पढ़ना"। अनुमान विधि (प्रमुख) समीकरणों के बाएँ और दाएँ पक्षों में शामिल कार्यों की सीमा का उपयोग करना।

शैक्षिक और विषयगत योजना

प्रति कार्यक्रमवैकल्पिक पाठ्यक्रम"समीकरणों को हल करने के गैर-मानक तरीके"ग्रेड 11

अनुबंध।

विषय 1. "परिचय"

समीकरण ए = बी दो गणितीय अभिव्यक्तियों ए और बी की समानता है, जिसमें शामिल हैं: एक या अधिक परिवर्तनीय मात्रा। चर के संबंध में, यह इंगित किया जाना चाहिए कि उनमें से कौन अज्ञात (मूल) माना जाता है, और कौन से ज्ञात (पैरामीटर) हैं। समीकरण में शामिल अज्ञातों की संख्या के आधार पर, इसे एक, दो के साथ, आदि के साथ समीकरण कहा जाता है। अनजान। जब तक अन्यथा निर्दिष्ट न हो, अभिव्यक्ति ए और बी को उनमें शामिल चर के संख्यात्मक मानों के सेट पर माना जाता है, जिसके लिए वे एक साथ समझ में आते हैं, अर्थात। सभी निर्दिष्ट क्रियाएं संभव हैं। वेरिएबल्स के वे मान जिनके लिए एक्सप्रेशन ए और बी एक साथ समझ में आते हैं, वेरिएबल के स्वीकार्य मान कहलाते हैं।एक अज्ञात x के साथ एक समीकरण पर विचार करें: f (x) = (x), जहां f (x) और φ (x) एक चर x के कुछ फलन हैं। इस समीकरण का हल, या मूल, संख्या x0 है, समीकरण के दोनों पक्षों में x के स्थान पर इसे प्रतिस्थापित करने पर सही समानता प्राप्त होती है (अर्थात x = x0 के लिए, फलन f (x), (x) ) परिभाषित हैं और उनके मूल्य मेल खाते हैं)। समीकरण की जड़ x के स्वीकार्य मानों के समुच्चय (क्षेत्र) से संबंधित है। किसी समीकरण को हल करने का अर्थ है उसके सभी हलों का समुच्चय खोजना या यह दिखाना कि उसका कोई हल नहीं है।

समीकरणों को हल करने की विधियाँ समीकरणों की तुल्यता (समतुल्यता) की अवधारणा पर आधारित हैं। दो समीकरण f1 (x) = φ1 (x) और f2 (x) = 2 (x) समतुल्य (समतुल्य) कहलाते हैं यदि उनके सभी हलों के समुच्चय मेल खाते हों या यदि दोनों समीकरणों का कोई हल न हो। इसलिए, यदि पहले समीकरण का प्रत्येक मूल दूसरे का मूल है और, इसके विपरीत, दूसरे समीकरण का प्रत्येक मूल पहले का मूल है, तो समीकरण समतुल्य हैं: f1 (x) = φ1 (x) ↔ f2 ( एक्स) = 2 (एक्स)।

समतुल्य समीकरणों की परिभाषा केवल उनके समाधान के सेट से जुड़ी होती है। अज्ञात के स्वीकार्य मूल्यों की विभिन्न श्रेणियों वाले समीकरण भी समतुल्य हो सकते हैं। दो समीकरण समतुल्य या समतुल्य नहीं हो सकते हैं, यह इस बात पर निर्भर करता है कि उन्हें किस संख्या के सेट (वास्तविक या जटिल) पर विचार किया जाता है। यहां कुछ उदाहरण दिए गए हैं।

. समीकरण एक्स - 2 = 1 और (एक्स - 2) (एक्स 2 + 1) = एक्स 2 + 1 वास्तविक संख्याओं के समुच्चय के समतुल्य हैं, क्योंकि उनके पास केवल 3 के बराबर एक वास्तविक मूल है। सम्मिश्र संख्याओं के समुच्चय पर, वे समतुल्य नहीं हैं, क्योंकि दूसरे समीकरण में, 3 के बराबर मूल के अतिरिक्त, ± i के बराबर काल्पनिक जड़ें।

दो समीकरण एफ 1 (एक्स) = 1 (एक्स) और एफ 2 (एक्स) = 2 (एक्स)कहा जाता है समतुल्य) कुछ सेट M . के संबंध में (सेट एम पर) यदि उनके पास इस सेट पर समान समाधान हैं या यदि दोनों के पास इस सेट पर कोई समाधान नहीं है।

इस दृष्टि से, समीकरण x 2 - 4 = 0 और x - 2 = 0 समुच्चय R + पर तुल्य हैं, x-2 = 0 और (x - 2) 2 = 0 समुच्चय R, f पर तुल्य हैं। 2 (x) = φ 2 (x) और f (x) = f (x) सेट M पर समतुल्य हैं, जहां f (x) और f (x) साइन-स्थिर हैं (समान चिह्न बनाए रखें, अर्थात सकारात्मक रहें) या एक ही समय में नकारात्मक)।

यदि पहले समीकरण के सभी मूल एफ 1 (एक्स) = एफ 1 (एक्स)समीकरण f 2 (x) = f 2 (x) की जड़ों के समूह से संबंधित है, तो इसे कहा जाता है पहले समीकरण का परिणामऔर लिखा

एफ 1 (एक्स) = एफ 1 (एक्स)→ एफ 2 (एक्स) = एफ 2 (एक्स)।

यदि, समाधान के दौरान, कोई समीकरण से उसके उपफल तक जाता है, तो कोरोलरी की जड़ों की जांच करना आवश्यक है, जिसमें वे भी शामिल हैं जो अज्ञात प्रारंभिक समीकरण के स्वीकार्य मूल्यों की सीमा में शामिल हैं। दरअसल, मूल समीकरण की जड़ों के अलावा, उपफल के समाधान के सेट में ऐसे समाधान भी शामिल हो सकते हैं जो मूल समीकरण की जड़ें नहीं हैं (उदाहरण के लिए, समीकरण के दोनों पक्षों को समान शक्ति तक बढ़ाने के बाद)। ऐसे समाधान कहलाते हैं मूल समीकरण के लिए बाहरी लोग।

विषय 2. संपूर्ण परिमेय समीकरण।

परिभाषा 1.समीकरणएफ(x) = g (x), जहां फलन f (x) और g (x) संपूर्ण परिमेय व्यंजकों द्वारा दिए गए हैं, संपूर्ण परिमेय समीकरण कहलाते हैं।

ओ.डी.जेड. इस समीकरण का सभी वास्तविक संख्याओं का समुच्चय है। समरूप परिवर्तनों का उपयोग करते हुए किसी भी पूर्ण परिमेय व्यंजक को बहुपद के रूप में निरूपित किया जा सकता है, तो यह समीकरण समीकरण P (x) = के तुल्य है।क्यू(एक्स), जहां पी (एक्स) और क्यू (एक्स) एक चर एक्स के साथ कुछ बहुपद हैं। क्यू (एक्स) को बाईं ओर ले जाने पर, हम समकक्ष समीकरण पी (एक्स) - क्यू (एक्स) = 0 प्राप्त करते हैं।

समीकरण के बाईं ओर बहुपद की घात को संपूर्ण परिमेय समीकरण की घात कहा जाता है। संपूर्ण परिमेय समीकरण को हल करने से समीकरण के बाईं ओर बहुपद के मूल ज्ञात हो जाते हैं। डिग्री बहुपदएन n से अधिक भिन्न मूल नहीं हो सकते हैं, इसलिए डिग्री n के किसी भी संपूर्ण परिमेय समीकरण में अधिकतम n मूल होते हैं।

हम रैखिक और . के मूल ज्ञात करने के सूत्र जानते हैं द्विघातीय समीकरण... अन्य समीकरणों को हल करने की प्रक्रिया दिए गए समीकरण को उपरोक्त समीकरणों में कम करना है। इसके लिए, दो मुख्य विधियों का उपयोग किया जाता है: 1) गुणनखंडन, 2) एक नए चर का परिचय।

एक)। फैक्टरिंग विधि।

प्रमेय 1... समीकरणएफ(x) g (x) = 0 पूर्ण संख्या अक्ष पर परिभाषित समीकरण f (x) = 0 और g (x) = 0 के समुच्चय के बराबर है।

प्रमेय 1 के अनुसार, समीकरणों का हल इसके बायीं ओर के गुणनखंड से निकटता से संबंधित है। यह विधि आपको डिग्री के पूरे समीकरण के समाधान को कम करने की अनुमति देती हैएनकम डिग्री के संपूर्ण समीकरणों को हल करने के लिए।

उदाहरण 1।समीकरण को हल करें 2x 3 - 3x 2 - 8x + 12 = 0

हल: आइए समूहीकरण विधि द्वारा बायीं ओर बहुपद का गुणनखंड करें:

2x 3 - 3x 2 - 8x + 12 = x 2 (2x-3) - 4 (2x - 3) = (2x - 3) (x 2 -4)।

तब मूल समीकरण समीकरण (2х - 3) (х 2 -4) = 0 के बराबर होता है, जो प्रमेय 1 के अनुसार समीकरणों 2х - 3 = 0 और х 2 - 4 = 0 के समुच्चय के बराबर है। उन्हें हल करने पर, हम प्राप्त करते हैं: x 1 = 1.5, x 2 = 2, x 3 = - 2।

उत्तर: -2; 1.5; 2.

प्रमेय 2. यदि पूर्णांक गुणांकों वाले एक संपूर्ण परिमेय समीकरण के पूर्णांक मूल हैं, तो वे इस समीकरण के मुक्त पद के भाजक हैं।

प्रमेय 3. यदि =  - समीकरण का हलएफ(एक्स) = 0,

फिर च(एक्स) = (एक्स-) एफ 1 (एक्स)।

यह समीकरण सेट x = और . के बराबर हैएफ 1 (x) = 0, जहां f 1 (x) = 0 डिग्री n-1 का समीकरण है, अर्थात। एक निचली डिग्री। उदाहरण 3.समीकरण x 4 - 4x 3 - 13x 2 + 28x +12 = 0 हल करें।

समाधान। मुक्त सदस्य के भाजक हैं

1, 1, -2, 2, -3, 3, -4, 4, -6, 6, -12, 12.

हॉर्नर की योजना का उपयोग करके, हम जांच करेंगे कि इन संख्याओं के बीच इस समीकरण की कोई जड़ें हैं या नहीं।

हम इस समीकरण को इस रूप में निरूपित करते हैं: (x-1) (x + 3) (x 2 - 5x -2) = 0।

यह इस प्रकार है कि x 1 = 2, x 2 = -3, x z =, x 4 =
.

उत्तर: x 1 = 2, x 2 = -3, x z =, x 4 =।

2) परिवर्तनीय प्रतिस्थापन विधि।

एक नए चर को पेश करने की विधि यह है कि समीकरण को हल करने के लिएएफ(x) = 0 एक नया चर y = q (x) पेश करें और f (x) को y के रूप में व्यक्त करें, एक नया समीकरण प्राप्त करें, जिसे हल करके, मूल चर पर वापस आ जाएं।

उदाहरण 4. समीकरण (3x + 2) 4 - 13 (3x + 2) 2 +36 = 0 को हल करें।

समाधान। y = (3x + 2) 2 सेट करने पर, हम समीकरण प्राप्त करते हैं

वाई 2 - 13y +36 = 0

इसके मूल ज्ञात कीजिए: y 1 = 4, y 2 = 9, और समीकरणों को हल करें

(3x +2) 2 = 4 और (3x +2) 2 = 9

हमें उत्तर मिलता है: x 1 = 0, x 2 = -, x 3 =, x 4 = -।

उदाहरण 5. समीकरण (x + 1) (x + 2) (x + 3) (x + 4) = 24 . को हल कीजिए

समाधान। आइए पहले कारक को अंतिम के साथ और दूसरे को तीसरे के साथ समूहीकृत करते हुए कोष्ठक का विस्तार करें: (x 2 + 5x + 4) (x 2 + 5x + 6) = 24.

x 2 + 5x = y को सेट करने पर, हमें दूसरी डिग्री (y + 4) (y + 96) = 24 का एक समीकरण मिलता है, जिसे हल करने पर हमें समीकरण y 2 + 10y = 0 प्राप्त होता है, जहाँ से y = 0 या y = -10. मूल चर x पर लौटने पर, हमें दो समीकरण मिलते हैं:

x 2 + 5x = 0 और x 2 + 5x = -10।

पहले समीकरण की जड़ें 0 और -5 हैं, दूसरे की कोई जड़ नहीं है, क्योंकि इसका विवेचक हैडी

उत्तर: -5; 0.

3) विपरीत समीकरण

कई समीकरणों को हल करते समय यह अनुमान लगाना कठिन होता है कि समीकरण को सरल बनाने के लिए कौन सा नया चर शामिल किया जाना चाहिए। इसलिए, विभिन्न प्रकार के संपूर्ण तर्कसंगत समीकरणों पर विचार किया जाता है, जिनके सरलीकरण के लिए एक प्रतिस्थापन जाना जाता है।

इस तरह के समीकरणों में पारस्परिक समीकरण, सममित समीकरण, सजातीय समीकरण शामिल हैं।

चौथी डिग्री के पारस्परिक समीकरण हैं:

कुल्हाड़ी 4 + 3 में + सीएक्स 2 + में + ए = 0।

एक नया चर y = x + पेश करने से, यह समीकरण एक वर्ग तक कम हो जाता है।

इसी तरह, एक नया चर y = x + पेश करते हुए, कोई भी फॉर्म के समीकरणों को सरल बना सकता है

कुल्हाड़ी 4 + 3 में + सीएक्स 2 + के+ के 2 ए = 0 में। ऐसे समीकरणों को सामान्यीकृत चतुर्थ-डिग्री आवर्तक समीकरण कहा जाता है।

उदाहरण 6. समीकरण 3x 4 -2x 3 + 4x 2 -4x + 12 = 0 . को हल करें

समाधान। यह k = 2 के साथ चौथी डिग्री का सामान्यीकृत रिटर्न समीकरण है, क्योंकि 3x 4 - 2x 3 + 4x 2 - 2 2x + 3 ∙ 2 2 = 0।

चूँकि x = 0 इस समीकरण का मूल नहीं है, हम समीकरण के दोनों पक्षों को x 2 0 से विभाजित करते हैं और समीकरण के पदों को सिरों से समान दूरी पर समूहित करते हैं।

,

हम रखतें है
= y, तब
= y 2, और इसलिए
= y 2 -4, इसे समीकरण में प्रतिस्थापित करें, हमें एक द्विघात समीकरण प्राप्त होता है: 3 (y 2 -4) - 2y + 4 = 0, जहाँ से हमें मूल मिलते हैं

वाई 1 = 2, वाई 2 = -।

अब समस्या समीकरणों के एक सेट में सिमट गई है:

2 .

इन समीकरणों का कोई वास्तविक मूल नहीं है, जिसका अर्थ है कि दिए गए समीकरण का कोई मूल नहीं है।

उत्तर: कोई जड़ें नहीं हैं।

पांचवीं डिग्री के पारस्परिक समीकरण का रूप है: कुल्हाड़ी 5 + में 4 + सीएक्स 3 + सीएक्स 2 + में + ए = 0,

छठी डिग्री: आह 6 + 5 में + सीएक्स 4 +डीएक्स 3 + सीएक्स 2 + में + ए = 0, आदि।

लियोनार्ड यूलर (1707-1783) ने सिद्ध किया कि विषम अंश के किसी भी आवर्तक समीकरण का मूल -1 होता है और ऐसे समीकरण को x + 1 से विभाजित करने पर सम अंश का समीकरण प्राप्त होता है, जो आवर्तक भी होगा। उन्होंने यह भी सिद्ध किया कि सम घात के प्रत्येक आवर्त समीकरण, मूल x = के साथ, में मूल x = . भी होता है .

4) सजातीय समीकरण

फॉर्म पी का एक समीकरण (तुम, v) = 0 u और v के संबंध में घात k का एक समांगी समीकरण कहलाता है, यदि (u, v) घात k का एक समांगी बहुपद है। u और v के संबंध में k घात का समांगी समीकरण इसका गुण है कि यदि हम समीकरण के सभी पदों को विभाजित करते हैं kth डिग्रीचरों में से एक, तो यह एक चर के साथ डिग्री k के समीकरण में बदल जाता है।

उदाहरण 8... प्रश्न हल करें

(x 2 + x + 1) 3 + 2x 4 (x 2 + x +1) - 3x 6 = 0

समाधान। आइए नए चर पेश करते हैंतुम= x 2 + x + 1, v = x 2, हमें प्राप्त होता है सजातीय समीकरणयू 3 + 2यूवी 2 3वी 3 = 0। यह जाँचने के बाद कि x = 0 मूल समीकरण का मूल नहीं है, हम परिणामी समीकरण को v 3 = x 6 से विभाजित करते हैं।

हमें समीकरण मिलता है
+ 2
-3 =0.

हम रखतें है
, हम समीकरण y 3 + 2y - 3 = 0 हल करते हैं।

यह देखना आसान है कि y = 1 एक मूल है, इसलिए बहुपद को विभाजित करना

y 3 + 2y - 3 पर (y-1), हम समतुल्य समीकरण को पास करते हैं

(y-1) (y 2 + y +3) = 0, जिसका एक वैध मूल y = 1 है।

इसलिए, यह समीकरण को हल करने के लिए बनी हुई है
.

इस समीकरण को हल करने पर हमें केवल एक ही मूल x = 1 प्राप्त होता है।

उत्तर 1।

5) समीकरणों को हल करते समय अपरिभाषित गुणांकों की विधि का अनुप्रयोग।

उदाहरण 9. आइए समीकरण हल करें एक्स 4 + एक्स 3 - 4एक्स 2 - 9एक्स- 3 = 0.

समाधान:मान लीजिए कि समीकरण की जड़ें पूर्णांक हैं, तो उन्हें ± 1; ± 3 संख्याओं के बीच खोजा जाना चाहिए।

अगर एक्स= 1, तो
अगर एक्स= -1, तब
अगर एक्स= 3, तब
अगर एक्स= -3, तब

इसलिए हम यह निष्कर्ष निकालते हैं कि तर्कसंगत जड़ेंहमारे समीकरण नहीं है।

आइए बहुपद कारकों का विस्तार करने का प्रयास करें निम्नलिखित नुसार: , कहाँ पे ए, बी, सीतथा डी- पूरा का पूरा। आइए कोष्ठक का विस्तार करें:

ए, बी, सीतथा डीहम समीकरणों की एक प्रणाली प्राप्त करते हैं:

चूंकि बीडीओ= -3, तो हम विकल्पों में से समाधान खोजेंगे:

आइए विकल्प संख्या 2 की जाँच करें, जब ख = -एक; डी = 3:

ए= -2, साथ =3

उत्तर;

उदाहरण 10. प्रश्न हल करें: एक्स 4 - 15एक्स 2 + 12एक्स+ 5= 0.

समाधान: हम बहुपद का विस्तार करते हैं च (एक्स) = एक्स 4 - 15एक्स 2 + 12एक्स+5 निम्नलिखित रूप में गुणनखंडों द्वारा:, जहां ए, बी, सीतथा डी- पूर्णांक। आइए कोष्ठक का विस्तार करें:

अज्ञात के लिए व्यंजकों के संगत गुणांकों की बराबरी करना ए, बी, सीतथा डीहम समीकरणों की एक प्रणाली प्राप्त करते हैं:

चूंकि, बीडीओ= 5, तब हम विकल्पों में से समाधान खोजेंगे:

सिस्टम विकल्प संख्या 2 से संतुष्ट है, अर्थात। ए= 3, बी = -1, सी = -3, डी= 5.

इसलिए,

उत्तर :

6) पैरामीटर परिचय विधि

गणना की प्रक्रिया को सरल बनाने के लिए या मूल अभिव्यक्ति को एक ऐसा रूप देने के लिए जो निर्णय लेने के लिए अधिक सुविधाजनक है, एक सहायक चर को पेश करने के सबसे सामान्य तरीकों में से एक संख्या या संख्यात्मक अभिव्यक्तियों के विभिन्न प्रकार के पदनाम हैं।

उदाहरण 11.एक समीकरण को हल करें और उसके सभी हलों का योग ज्ञात करें

एक्स 4 -12 एक्स 2 +16
एक्स - 12 = 0

समाधान। यदि हम पैरामीटर = s का परिचय देते हैं, तो मूल समीकरण रूप लेता है

X 4 - 6 में 2 x 2 + 8 में 3 x - 3 में 4 = 0,

या परिवर्तन के बाद (x - b) 2 (x 2 + 2in -3v 2) = 0

इसलिए यह दिखाना आसान है कि इस समीकरण के दो हल हैं और -3, और उनका योग -2 है।

उत्तर: -2।

विषय 2.भिन्नात्मक परिमेय समीकरण.

परिभाषा। एक चर में समीकरणएफ(एक्स) = जी (एक्स), जहां एफ (एक्स) और जी (एक्स) हैं तर्कसंगत अभिव्यक्ति, जिनमें से कम से कम एक में शामिल है बीजीय भिन्न, भिन्नात्मक परिमेय कहलाता है।

कुछ भी भिन्नात्मक परिमेय समीकरण 0 . कर सकते हैं

यदि सभी वास्तविक x बहुपद के लिएक्यू(x) 0, फिर, यह ध्यान में रखते हुए कि अंश 0 के बराबर है, केवल उस स्थिति में जब इसका अंश 0 के बराबर होता है, हम समतुल्य तर्कसंगत समीकरण P (x) = 0 को पास करते हैं, जिसमें सभी जड़ों को पाया जाता है जो, हम मूल समीकरण के मूल भी ज्ञात करेंगे।

यदि, x . के कुछ मानों के लिएक्यू(x) = 0, तो समीकरण P (x) = 0 इस समीकरण का केवल एक परिणाम है, इसलिए इसके सभी मूलों को बहुपद Q (x) में प्रतिस्थापित किया जाना चाहिए और उन मूलों को छोड़ देना चाहिए जिनके लिए Q (x) = 0 है।

इसलिए, किसी भी भिन्नात्मक परिमेय समीकरण को संपूर्ण परिमेय समीकरण में घटाया जा सकता है। हालांकि, यह हमेशा तुरंत करने की आवश्यकता नहीं है। कुछ मामलों में, पहले गुणनखंडन या परिवर्तनशील परिवर्तन पद्धति को लागू करने की सलाह दी जाती है।

उदाहरण 1. समीकरण को हल करें:

उपाय। समीकरण के दोनों ओर अनियमित परिमेय भिन्न। सबसे पहले, प्रत्येक भिन्न में संपूर्ण भागों का चयन करें और फिर सभी पदों को बाईं ओर स्थानांतरित करें:

इसलिए, मूल समीकरण समीकरण के बराबर है:

सभी पदों को बाईं ओर स्थानांतरित करने पर, हमें एक समान समीकरण मिलता है

जिसे हल करने पर हम मूल x 1 = -1, x 2 = 0.25 पाते हैं। चूँकि भिन्न का हर इन मानों के लिए लुप्त नहीं होता है, x के ये मान मूल समीकरण के मूल हैं।

उत्तर 1; 0.25.

उदाहरण 2. समीकरण को हल करें:

हम इस समीकरण को समान व्यंजक के जोड़ और घटाव के साथ प्रतिस्थापित करते हैं

आइए हम अंश का गुणनखंड करें

जिनके मूल x = ± 5 हैं।

बहुपद को बहुपद से भाग देकर इस समीकरण को दूसरे तरीके से हल किया जा सकता है.

उदाहरण 3. समीकरण को हल करें:

समीकरण के दोनों पक्षों को से भाग देने पर , 0 इस समीकरण का हल नहीं है):

ये मानते हुए
, हम समीकरण (y-3) (y-4) = 12 प्राप्त करते हैं; y²-7y = 0

जिनके मूल y = 0 और y = 7 हैं।

माध्यम,
या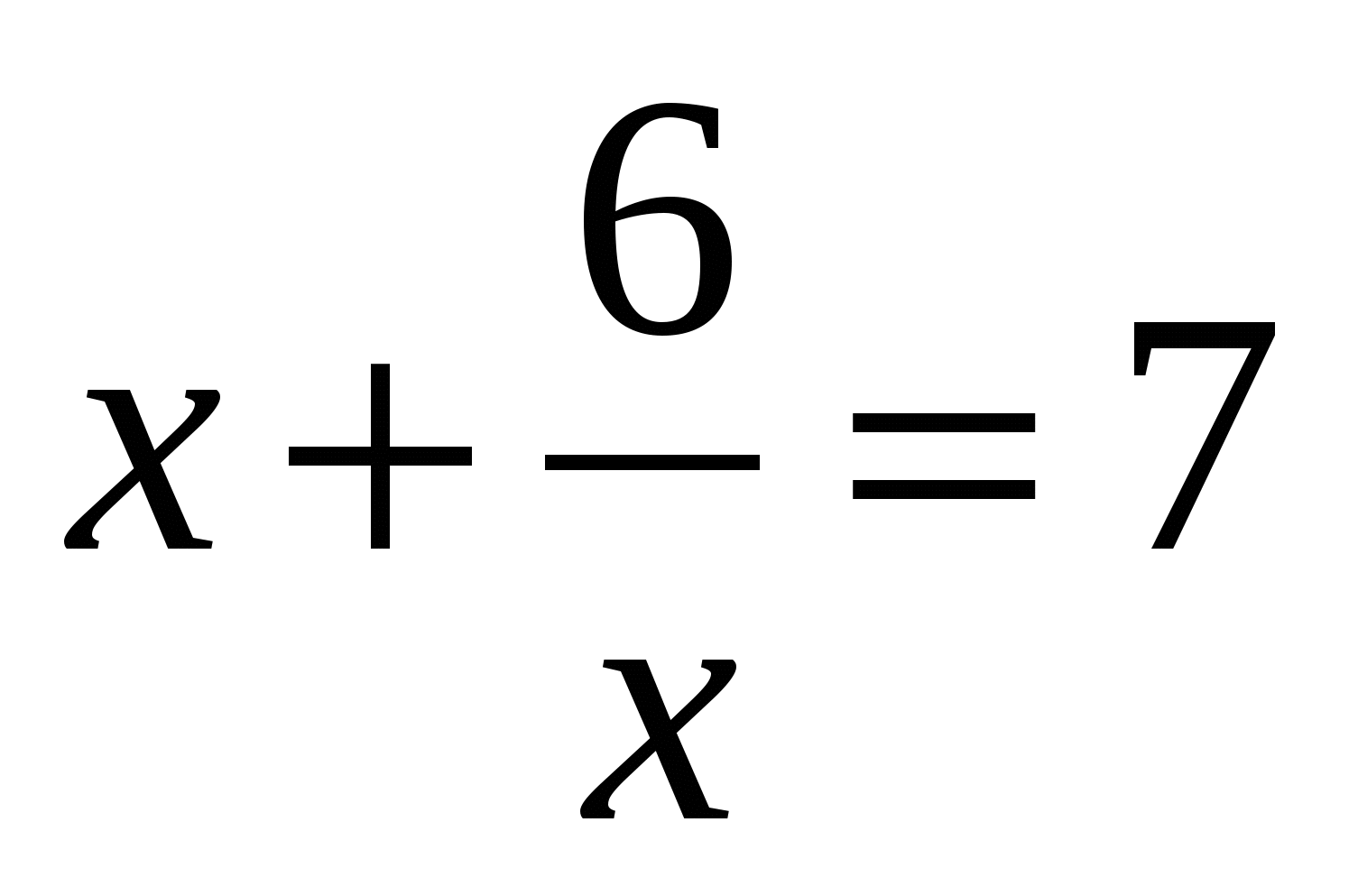
... पहले समीकरण का कोई मूल नहीं है, और दूसरे समीकरण का मूल हैएक्स = 6 और एक्स = 1।

यह उदाहरणयह दर्शाता है कि समीकरण के दोनों पक्षों को एक ही व्यंजक से विभाजित करने के बाद प्रतिस्थापन की शुरूआत के साथ समीकरण की डिग्री को कम करने की अनुमति मिलती है।

उदाहरण 5. समीकरण को हल करें:

इस समीकरण के स्वीकार्य मूल्यों की सीमा सभी संख्याएं हैं जो शर्त को संतुष्ट करती हैं

फिर,

होने देना

इस भिन्नात्मक परिमेय समीकरण को हल करने पर, हम मूल प्राप्त करते हैं

माध्यम, ।

समीकरणों के हल हैं

उदाहरण 6. समीकरण को हल करें:

ओडीजेड:

होने देना
टी-1.

परिवर्तन करते हुए, यह समीकरण रूप में कम हो जाता है

.

इस समीकरण की जड़ें
इसलिए,

TOPIC4 समीकरणों को हल करते समय कार्यों के गुणों का अनुप्रयोग

²

1) दायरे का उपयोग करना.

प्रश्न हल करें:

समाधान।पहला रेडिकल 1-х²≥0 पर परिभाषित किया गया है, अर्थात। -1≤x≤1।

दूसरे रेडिकल को किसी भी x के लिए परिभाषित किया गया है। तीसरे रेडिकल के तहत अभिव्यक्ति गैर-ऋणात्मक है यदि x + 2x-3≥0यानी x≤-3 और x≥1 पर।

एकमात्र बिंदु जिस पर इन रेडिकल्स को परिभाषित किया गया है, वह है x = 1। यह जाँचना आसान है कि यह संख्या समीकरण का मूल है।

उत्तर 1

प्रश्न हल करें:।

हल: 1) समीकरण के बाईं ओर फलन के अस्तित्व के लिए शर्त लिखिए:। इस असमानता को दूर करना काफी कठिन है।

2) आइए दाईं ओर देखें: -1-2x²≥0.2x²≤-1। अंतिम असमानता का कोई समाधान नहीं है।

3) इसलिए, मूल समीकरण का भी कोई हल नहीं है, क्योंकि इसका बायां हाथ एक गैर-ऋणात्मक कार्य है।

उत्तर: खाली सेट।

2 ) एकरसता का उपयोग करना

प्रश्न हल करें :

हल: यह समीकरण संख्या x = 2 से संतुष्ट होता है। आइए देखें कि क्या समीकरण बनाने वाले फलन उन शर्तों को पूरा करते हैं जिनके तहत यह तर्क दिया जा सकता है कि कोई अन्य मूल नहीं हैं। पहले विचार करें ... आइए हम व्युत्पन्न का उपयोग करके एकरसता के लिए इसकी जांच करें: . द्विघात समीकरण को हल करना

,

इसीलिए
x के सभी मानों के लिए, इसलिए फलन f (x) बढ़ रहा है।

आइए अब फ़ंक्शन की जांच करें
... यह स्थापित करना आसान है कि यह x के सभी मानों के लिए घटता है। अध्ययन से, हम यह निष्कर्ष निकाल सकते हैं कि x = 2 इस समीकरण का एकमात्र मूल है।उत्तर: एक्स = 2

जड़ प्रमेय।

चलो समारोह वाई = एफ (एक्स)सेट पर बढ़ता (या घटता)(एफ),संख्या ए- स्वीकृत मूल्यों में से कोई भी च (एक्स)मंच पर एक्स , फिर समीकरण एफ (एक्स) = एसेट पर एक अनूठी जड़ है एक्स।

सबूत:

बढ़ते कार्य पर विचार करें च (एक्स)(घटते कार्य के मामले में, तर्क समान है)। परिकल्पना से, सेट पर एक्स एक ऐसा नंबर है बी, क्या एफ (बी) = ए... आइए दिखाते हैं कि बीसमीकरण का एकमात्र मूल है एफ (एक्स) = ए.

मान लीजिए कि सेट पर एक्स अभी भी एक संख्या है , ऐसा है कि च (सी) = ए... तो कोई सी बी, या सी> बी... लेकिन समारोह च (एक्स)सेट पर बढ़ जाती है एक्स , इसलिए, क्रमशः, या तो च (सी), या एफ (सी)> एफ (बी)... यह समानता के विपरीत है एफ (सी) = एफ (बी) = ए... नतीजतन, यह धारणा भी सेट पर गलत है एक्स संख्या को छोड़कर बी, समीकरण के अन्य मूल एफ (एक्स) = एनहीं।

इस कथन के आधार पर हम समीकरण को हल कर सकते हैं

एक्स 5 = 3 - 2xड्राइंग के बिना, निम्नलिखित एल्गोरिथम का पालन करें:

ध्यान दें कि के लिए एक्स = 1समानता रखती है 1 5 = 3-2 1,
साधन, एक्स = 1 -समीकरण की जड़ (हमने इस मूल का अनुमान लगाया);

समारोह वाई = 3 - 2xघटता है, और कार्य वाई = एक्स 5 यह बढ़ रहा है ,
तो जड़ है दिया गया समीकरणकेवल एक और
यह जड़ मूल्य है एक्स = 1.

उदाहरण। प्रश्न हल करें:

हल: सबसे पहले समीकरण को फॉर्म में लिखिए

,

तब हम मूल प्रमेय का प्रयोग करते हैं।

उत्तर : 5.

3) प्रमुख विधि

उन समस्याओं के लिए लागू जिसमें किसी समीकरण या असमानता के बाएँ और दाएँ पक्षों के मानों के समुच्चय में एक समान बिंदु होता है, जो एक भाग का सबसे बड़ा मान और दूसरे का सबसे छोटा मान होता है

ऐसी समस्याओं को हल करने के लिए, समीकरण को रूप में कम करें
दोनों भागों के लिए एक आकलन करें। यदि मानों की श्रेणी से कोई संख्या M है जैसे किएफ( x) M और g (x) M, तो समीकरण को दो समीकरणों के समतुल्य निकाय द्वारा प्रतिस्थापित किया जाता है
.

प्रश्न हल करें :

हल: आइए समीकरण के दाएं और बाएं पक्षों का अनुमान लगाएं:

ए),
चूंकि, x² + 4x + 13≥9, और

बी)
, चूंकि
.

समीकरण के भागों के मूल्यांकन से पता चलता है कि बाईं ओर कम नहीं है, और चर x के किसी भी स्वीकार्य मान के लिए दाहिना पक्ष दो से अधिक नहीं है। इसलिए, यह समीकरण प्रणाली के बराबर है

निकाय के पहले समीकरण का केवल एक मूल x = -2 है। इस मान को दूसरे समीकरण में प्रतिस्थापित करने पर, हमें सही संख्यात्मक समानता प्राप्त होती है:

... उत्तर 2

प्रश्न हल करें

समाधान:समीकरण को हल करने के लिए, हम भागों का अनुमान लगाते हैं:
;
/

एक और एक ऋणात्मक संख्या का योग है, इसलिए समानता तभी संभव है जब
/

सबसे पहले, हम दूसरा समीकरण हल करते हैं
,
,

, x² + x = 0.इस समीकरण के मूल x = 0 और x = -1 हैं।

आइए हम इन जड़ों को रखकर पहली समानता की वैधता की जाँच करें।

x = 0 के लिए, हमें सही समानता मिलती है, x = -1 के लिए - गलत। अत: इस समीकरण का एक ही मूल x = 0 है।

परिशिष्ट 2

स्वतंत्र समाधान के लिए समस्याएं

एक) "संपूर्ण तर्कसंगत समीकरण

x 4 - 8x - 57 = 0

4.x 3 - x 2 -8x + 12 = 0

x 3 + 2x 2 + 3x = 6

5. x 3 -9 x 2 + 27x - 27 = 0

x 4 + 2x 3 - 25 x 2 - 26x = -120

6.x 4 + 2x 3 - 16x 2 - 2x + 15 = 0।

x 3 -3x 2 - 3x + 1 = 0.

(एक्स +1) (एक्स +3) (एक्स +5) (एक्स +7) = -15

.x 4 - 3x 2 +2 = 0

... 2 (x 2 + x +1) 2 - 7 (x -1) 2 = 13 (x 3 - 1)

.x 4 + 4x 3 - x 2 -16x - 12 = 0

... x 4 -5x 3 + 10x 2 - 10x + 4 = 0

(एक्स 2 + एक्स) 2 + 4 (एक्स 2 + एक्स) -12 = 0

(x +5) 4 - 13 x 2 (x + 5) 2 + 36 x 4 = 0

पैरामीटर परिचय विधि

1.y 4 - 2
वाई 2 - वाई + 3 - = 0

2. (y 2 + 5y +1) 2 + 6y (y 2 + 5y +1) + 8y 2 = 0

3.a 2 - 2 (x 2 - 5x -1) a + x 4 - 10 x 3 + 22x 2 + 12x = 0

2) « समीकरणों को हल करने के लिए कार्यों के गुणों को लागू करना »

पहला स्तर।

समीकरण हल करें:

1.
(उत्तर: 0);

2.
(उत्तर: 2);

3.
(उत्तर: 3);

4.
(उत्तर - 4);

5.
(उत्तर: -2);

6.
(उत्तर 1)।

दूसरा स्तर।

समीकरण हल करें:

1. (उत्तर 1);

2.
(उत्तर 1);

3.
(उत्तर: -2);

4.
(उत्तर: 2)

5.
(उत्तर: -3);

6.
(उत्तर: -2);

7. (उत्तर: 2)।

8. उत्तर:

10.
उत्तर; 0

11.
उत्तर: 0.5

12. उत्तर 1

टेक्ट " चित्रमय विधिसमीकरण हल करना "

मैंस्तर

1. समीकरण x 2 + 4x = x 3 का मूल है:

ए) -2 बी) -1 सी) 0 डी) 1 ई) 2

2. समीकरण के मूलों का योग एक्स 2 -x-3 = 3 बराबर:

ए) 4 बी) 2 सी) -4 डी) 0 ई) -2

3. समीकरण के मूलों का गुणनफल -0.5x 2 + 3 = x 2 -3

ए) 2 बी) 1 सी) 6 डी) -2 ई) -4

4. समीकरण 2√ . के मूल एक्स= 2x अंतराल के हैं:

ए) बी) [-1; 1] सी) (0; 1] डी) के बराबर है:

ए) -12 बी) 12 सी) -6 डी) -9 ई) 8

2. समीकरण के मूलों के निरपेक्ष मानों का योग- (√ (5-) एक्स) (5 + x)) + 2 = -1

के बराबर है:

ए) 4 बी) 8 सी) 7 डी) 5 ई) 9

3. समीकरण जड़ें एक्स 4 = | (- | एक्स | +1) 2 -1 | सेट से संबंधित हैं:

ए) (- 1; 1) बी) [-1; 1] सी) (4; 11) डी) (- 1; 0; 1) ई) (0; 2]

4 *। का मान जिस पर समीकरण 2 / एक्स = ए- एक्स तीन जड़ें हैं, अंतराल को संदर्भित करता है:

ए) (3; + ) बी) [-1; 12] सी) (- ; 1) डी),तो यह जांचना आवश्यक है कि अंतराल के अंत में और प्रत्येक अंतराल में समीकरण या असमानता सत्य है, इसके अलावा, यदि ए< 0 , ए बी> 0, तो अंतराल पर जांचना जरूरी है (ए; 0) यू, खंड, अंतराल और आधा अंतराल।

उदाहरण 2.1.1 समीकरण को हल कीजिए

. (1)

समाधान। जाहिर है, तब से x ≤ 0 इस समीकरण का हल नहीं हो सकता है ... एक्स> 0 फ़ंक्शन के लिए इन x फलनों f (x) = x और . के लिए दो सतत धनात्मक सख्ती से बढ़ते फलनों के गुणनफल के रूप में निरंतर और सख्ती से बढ़ रहा है ... इसलिए, क्षेत्र में x> 0 फलन अपने प्रत्येक मान को ठीक एक बिंदु पर लेता है। यह देखना आसान है कि x = 1 इस समीकरण का हल है, इसलिए यह इसका एकमात्र हल है।

उत्तर 1)।

उदाहरण 2.1.2 असमानता को हल करें

. (2)

समाधान। प्रत्येक फलन y = 2 x, y = 3 x, y = 4 x संपूर्ण अक्ष पर निरंतर और सख्ती से बढ़ रहा है। इसका मतलब है कि मूल कार्य समान है ... यह देखना आसान है कि x = 0 के लिए फलन मान 3 लेता है। x> 0 के लिए इस फ़ंक्शन की निरंतरता और सख्त एकरसता के आधार पर, हमारे पास है , x . के लिए< 0 имеем ... इसलिए, इस असमानता के सभी हल x . हैं< 0.

उत्तर: (-∞;0) ।

उदाहरण 2.1.3 समीकरण को हल कीजिए

. (3)

समाधान। समीकरण (3) के स्वीकार्य मूल्यों की सीमा एक अंतराल है। ओडीजेड फ़ंक्शन तथा निरंतर और सख्ती से घट रहा है, इसलिए, निरंतर और घटते कार्य ... इसलिए, फ़ंक्शन h (x) अपने प्रत्येक मान को केवल एक बिंदु पर लेता है। चूँकि x = 2 मूल समीकरण का एकमात्र मूल है।

समीकरणों और असमानताओं को हल करते समय, वह गुण जो एक निश्चित सेट पर नीचे या ऊपर से एक फ़ंक्शन को बांधता है, अक्सर एक निर्णायक भूमिका निभाता है।

यदि कोई संख्या C ऐसी है कि असमानता f (x) C किसी के लिए भी धारण करती है, तो फ़ंक्शन f को सेट D (चित्र 2) पर ऊपर से घिरा हुआ कहा जाता है।

चित्र 2

यदि कोई संख्या c ऐसी मौजूद है कि असमानता f (x) c किसी के लिए भी धारण करती है, तो फ़ंक्शन f को सेट D (चित्र 3) पर नीचे से परिबद्ध कहा जाता है।

चित्र तीन

एक फ़ंक्शन जो ऊपर और नीचे दोनों ओर से घिरा होता है उसे सेट डी पर बाउंडेड कहा जाता है। सेट डी पर फ़ंक्शन f की ज्यामितीय रूप से बाध्यता का अर्थ है कि फ़ंक्शन y = f (x) का ग्राफ स्ट्रिप c ≤ y ≤ C (चित्र 4) में स्थित है। )

चित्र 4

यदि कोई फंक्शन सेट पर बाउंडेड नहीं होता है, तो कहा जाता है कि वह बाउंड नहीं है।

फ़ंक्शन का एक उदाहरण जो संपूर्ण संख्या अक्ष पर नीचे से घिरा हुआ है, फ़ंक्शन y = x 2 है। समुच्चय (-∞; 0) पर बंधित फ़ंक्शन का एक उदाहरण फ़ंक्शन y = 1 / x है। संपूर्ण संख्या अक्ष पर परिबद्ध फ़ंक्शन का एक उदाहरण y = sin x है।

उदाहरण 2.2.1 समीकरण को हल कीजिए

पाप (x 3 + 2x 2 + 1) = x 2 + 2x + 2. (4)

समाधान। किसी भी वास्तविक संख्या x के लिए हमारे पास sin (x 3 + 2x 2 + 1) ≤ 1, x 2 + 2x + 2 = (x + 1) 2 +1 1 है। चूंकि x के किसी भी मान के लिए बाईं ओर समीकरण एक से अधिक नहीं होता है, और दाहिनी ओर हमेशा कम से कम एक होता है, तो इस समीकरण का केवल समाधान हो सकता है।

कब, यानी। के लिए, समीकरण (4) का भी कोई मूल नहीं है।

उदाहरण 2.2.2 समीकरण को हल कीजिए

. (5)

समाधान। जाहिर है, x = 0, x = 1, x = -1 इस समीकरण के समाधान हैं। अन्य समाधान खोजने के लिए, फ़ंक्शन f (x) = = x 3 - x - sinπx की विषमता के कारण, x> 0, x ≠ 1 क्षेत्र में इसके समाधान खोजने के लिए पर्याप्त है, क्योंकि यदि x 0> 0 है उसका हल है, तो (-x 0) भी उसका हल है।

हम सेट x> 0, x ≠ 1 को दो अंतरालों में विभाजित करते हैं: (0; 1) और (1; + )

प्रारंभिक समीकरण को x 3 - x = sinπx के रूप में फिर से लिखें। अंतराल (0; 1) पर, फलन g (x) = x 3 - x केवल ऋणात्मक मान लेता है, क्योंकि x 3< < х, а функция h(x) = sinπx только положительные. Следовательно, на этом промежутке уравнение не имеет решений.

मान लीजिए x अंतराल (1; + ) से संबंधित है। x के इन मानों में से प्रत्येक के लिए, फ़ंक्शन g (x) = x 3 - x लेता है सकारात्मक मूल्य, फ़ंक्शन h (x) = sinπx विभिन्न संकेतों के मान लेता है, और फ़ंक्शन h (x) = sinπx अंतराल (1; 2] पर गैर-सकारात्मक है। इसलिए, अंतराल पर समीकरण का कोई समाधान नहीं है ( 1; 2)।

अगर x> 2, तो | sinπx | 1, x 3 - x = x (x 2 - 1)> 2 3 = 6, जिसका अर्थ है कि समीकरण का अंतराल (1; + ) पर भी कोई हल नहीं है।

तो, x = 0, x = 1 और x = -1 और केवल वे मूल समीकरण के समाधान हैं।

उत्तर: (-1; 0; 1)।

उदाहरण 2.2.3 असमानता को हल करें

समाधान। ODZ असमानताएँ x = -1 को छोड़कर सभी वास्तविक x हैं। हम ODZ असमानता को तीन सेटों में विभाजित करते हैं: -∞< x < -1, -1 < x ≤ 0, 0 < x < +∞ и рассмотрим неравенство на каждом из этих промежутков.

चलो -∞< x < -1. Для каждого из этих x имеем g(x) = < 0, а f(x) = 2 x >0. इसलिए, ये सभी x असमानता के समाधान हैं।

चलो -1< x ≤ 0. Для каждого из этих x имеем g(x) = 1 - , а f(x) = 2 x ≤ 1. Следовательно, ни одно из этих x не является решением данного неравенства.

चलो 0< x < +∞. Для каждого из этих x имеем g(x) = 1 - , a . Следовательно, все эти x являются решениями исходного неравенства.

उत्तर: .

एक फ़ंक्शन f (x) को आवर्त T 0 के साथ आवधिक कहा जाता है यदि दो शर्तें पूरी होती हैं:

· यदि, तो x + T और x - T भी परिभाषा D (f (x)) के क्षेत्र से संबंधित हैं;

किसी के लिए, समानता

एफ (एक्स + टी) = एफ (एक्स)।

तब से उपरोक्त परिभाषा से यह इस प्रकार है कि

यदि T फलन f (x) का आवर्त है, तो यह स्पष्ट है कि प्रत्येक संख्या nT, जहाँ, n 0, भी इस फलन का आवर्त है।

किसी फ़ंक्शन की सबसे छोटी सकारात्मक अवधि सकारात्मक संख्या T में सबसे छोटी होती है जो दिए गए फ़ंक्शन की अवधि होती है।

आवधिक कार्य ग्राफ

आवर्त फलन का ग्राफ आमतौर पर अंतराल पर बनाया जाता है, समीकरण (1) का कोई हल नहीं होता है।

यदि X> 2, तो sinпХ≤1, X3 - X = (X2 - 1)> 2 * 3 = 6, जिसका अर्थ है कि अंतराल पर (2; + ~) समीकरण (1) का भी कोई हल नहीं है। तो, एक्स = 0, एक्स = 1 और एक्स = -1, और केवल वे मूल समीकरण के समाधान हैं।

उत्तर: X1 = 0, X2 = 1, X3 = -1।

उदाहरण3: प्रश्न हल करें।

2 sinpX = X - n / 2 - X + n / 2। (2)

समाधान: हम = X - n / 2 - X + n / 2 को f (X) से निरूपित करते हैं। निरपेक्ष मान की परिभाषा से, यह निम्नानुसार है कि f (X) = n पर X≤ - n / 2, f (X) = -2X at - n / 2

अंतराल से X पर विचार करें (- n / 2, n / 2)। इस अंतराल पर समीकरण (2) को 2 sinnX = - 2X के रूप में अर्थात् रूप में पुनः लिखा जा सकता है।

सिनएक्स = - एक्स / एन। (3)

यह स्पष्ट है कि X = 0 समीकरण (3) का हल है, और इसलिए मूल समीकरण का। आइए हम सिद्ध करें कि अंतराल (- n/2; n/2) पर समीकरण (3) का कोई अन्य हल नहीं है।

एक्स 0 के लिए, समीकरण (3) समीकरण के बराबर है।

किसी भी मान XЄ (- / 2; 0) U (0; п / 2) के लिए, फ़ंक्शन f (X) = sinX / X केवल सकारात्मक मान लेता है, इसलिए, समीकरण (3) का सेट पर कोई समाधान नहीं है (- /2; 0) यू (0; एन/2)।

उत्तर: एक्स = 0; एक्स = (- 1) पीएन / 6 + पीएन, एन = 1.2 ...; = (- 1) एम + 1 पी / 6 + पीएम, एम = 1.2 ...

निष्कर्ष।

इस विषय के अध्ययन के दौरान, मैंने निम्नलिखित निष्कर्ष निकाला, समीकरणों को हल करने के गैर-मानक तरीके आपको अधिक तर्कसंगत तरीके से परिणाम प्राप्त करने की अनुमति देते हैं।

not . का उपयोग करते समय मानक तरीकेसमाधान में कम समय लगता है और यह अधिक रोचक भी है।

प्रयुक्त साहित्य की सूची।

,। "गणित में समस्याएं। समीकरण और असमानताएँ ”।

"मौखिक परीक्षा पर गणित"।

, "समीकरण समस्याएं"।

, "समीकरण और असमानताएँ"।

, "गणित। समस्याओं को हल करने के तरीके "।

सोलोविओव ए.एफ. "गणना की बराबरी करना"।

प्रकार