समरूपता की धुरी खींचना। केंद्रीय समरूपता

« समरूपता"- ग्रीक मूल का एक शब्द। इसका अर्थ है आनुपातिकता, एक निश्चित क्रम की उपस्थिति, भागों की व्यवस्था में पैटर्न।

प्राचीन काल से, लोगों ने चित्र, आभूषण और घरेलू वस्तुओं में समरूपता का उपयोग किया है।
समरूपता प्रकृति में व्यापक है। इसे पौधों की पत्तियों और फूलों के रूप में, जानवरों के विभिन्न अंगों की व्यवस्था में, क्रिस्टलीय निकायों के रूप में, एक फड़फड़ाती तितली में, एक रहस्यमयी बर्फ के टुकड़े, एक मंदिर में एक मोज़ेक, एक तारामछली में देखा जा सकता है।
अभ्यास, निर्माण और इंजीनियरिंग में समरूपता का व्यापक रूप से उपयोग किया जाता है। यह प्राचीन इमारतों, सामंजस्यपूर्ण प्राचीन ग्रीक फूलदानों, क्रेमलिन भवन, कारों, हवाई जहाजों और बहुत कुछ के रूप में एक सख्त समरूपता है। (स्लाइड 4) समरूपता के उपयोग के उदाहरण लकड़ी की छत और कर्ब हैं। (कर्ब और लकड़ी की छत के फर्श में समरूपता का उपयोग करने पर हाइपरलिंक देखें) आइए कुछ उदाहरण देखें जहां आप स्लाइड शो (आइकन शामिल करें) का उपयोग करके विभिन्न वस्तुओं में समरूपता देख सकते हैं।

परिभाषा: एक बिंदु के बारे में समरूपता है।
परिभाषा: यदि बिंदु O खंड AB का मध्यबिंदु है, तो बिंदु A और B किसी बिंदु O के प्रति सममित हैं।
परिभाषा: बिंदु O को आकृति की सममिति का केंद्र कहा जाता है, और आकृति को केंद्रीय सममिति कहा जाता है।
गुण: आकृतियाँ जो किसी बिंदु पर सममित होती हैं, समान होती हैं।
उदाहरण:

एक केंद्रीय सममित आकृति के निर्माण के लिए एल्गोरिदम
1. आइए एक त्रिभुज А 1В 1 С 1 का निर्माण करें, जो केंद्र (बिंदु) O के सापेक्ष त्रिभुज ABC के सममित है। ऐसा करने के लिए, बिंदुओं A, B, C को केंद्र O से कनेक्ट करें और इन खंडों को जारी रखें;
2. आइए खंडों एओ, बीओ, सीओ को मापें और बिंदु ओ के दूसरी तरफ अलग रखें, बराबर खंड (एओ = ए 1 ओ 1, बीओ = बी 1 ओ 1, सीओ = सी 1 ओ 1);

3. परिणामी बिंदुओं को सेगमेंट ए 1 बी 1 से कनेक्ट करें; ए 1 सी 1; बी1 सी 1.
प्राप्त 1 1 С 1 सममित ∆ABS।

- यह खींची गई धुरी (सीधी रेखा) के बारे में समरूपता है।
परिभाषा: बिंदु A और B किसी सीधी रेखा a के संबंध में सममित होते हैं, यदि ये बिंदु दिए गए बिंदु के लंबवत सीधी रेखा पर और समान दूरी पर स्थित हों।
परिभाषा: समरूपता के अक्ष को एक सीधी रेखा कहा जाता है जब झुकते समय "हिस्सों" का संयोग होता है, और आकृति को कुछ अक्ष के बारे में सममित कहा जाता है।
गुण: दो सममित आकृतियाँ समान होती हैं।
उदाहरण:

किसी सीधी रेखा के संबंध में सममित आकृति बनाने के लिए एल्गोरिदम
आइए एक त्रिभुज А1В1С1 की रचना करें, जो एक सीधी रेखा a के सापेक्ष एक त्रिभुज ABC के सममित है।
इसके लिए:
1. त्रिभुज ABC के शीर्षों से सीधी रेखा a पर लंबवत सीधी रेखाएँ खींचिए और उन्हें आगे भी जारी रखिए।
2. हम त्रिभुज के शीर्षों से सीधी रेखा पर परिणामी बिंदुओं तक की दूरी को मापते हैं और सीधी रेखा के दूसरी ओर समान दूरी को स्थगित करते हैं।
3. परिणामी बिंदुओं को सेगमेंट A1B1, B1C1, B1C1 से कनेक्ट करें।

प्राप्त A1B1C1 सममित ∆ABS।

(मतलब "आनुपातिकता") - कुछ परिवर्तनों के तहत ज्यामितीय वस्तुओं की संपत्ति को स्वयं के साथ जोड़ा जाना। "समरूपता" से तात्पर्य शरीर या आकृति की आंतरिक संरचना में किसी भी प्रकार की शुद्धता से है।

केंद्रीय समरूपता- एक बिंदु के बारे में समरूपता।

बिंदु के सापेक्षओह, यदि आकृति के प्रत्येक बिंदु के लिए बिंदु O के सापेक्ष इसके सममित बिंदु भी इस आकृति से संबंधित है। बिंदु O को आकृति की सममिति का केंद्र कहा जाता है।

वी एक आयामीअंतरिक्ष में (सीधी रेखा पर), केंद्रीय समरूपता दर्पण समरूपता है।

विमान पर (में 2-आयामीअंतरिक्ष) केंद्र ए के साथ समरूपता केंद्र ए के साथ 180 डिग्री रोटेशन है। एक विमान पर केंद्रीय समरूपता, रोटेशन की तरह, अभिविन्यास को संरक्षित करता है।

में केंद्रीय समरूपता तीन आयामीअंतरिक्ष को गोलाकार समरूपता भी कहा जाता है। इसे समरूपता के केंद्र से गुजरने वाले विमान के सापेक्ष प्रतिबिंब की संरचना के रूप में दर्शाया जा सकता है, जो समरूपता के केंद्र से गुजरने वाली सीधी रेखा के सापेक्ष 180 ° घुमाया जाता है और प्रतिबिंब के उपर्युक्त विमान के लंबवत होता है।

वी 4-आयामीअंतरिक्ष में, केंद्रीय समरूपता को समरूपता के केंद्र से गुजरने वाले दो परस्पर लंबवत विमानों के चारों ओर दो 180 ° घुमावों की संरचना के रूप में दर्शाया जा सकता है।

अक्षीय समरूपता- एक सीधी रेखा के बारे में समरूपता।

आकृति को सममित कहा जाता है अपेक्षाकृत सीधाए, यदि आकृति के प्रत्येक बिंदु के लिए वह बिंदु सममित है जो सीधी रेखा के सापेक्ष है और इस आकृति का भी है। रेखा a को आकृति की सममिति की धुरी कहा जाता है।

अक्षीय समरूपता दो परिभाषाएँ हैं:

- चिंतनशील समरूपता।

गणित में, अक्षीय समरूपता एक प्रकार की गति (दर्पण प्रतिबिंब) है जिसमें निश्चित बिंदुओं का समूह एक सीधी रेखा है, जिसे समरूपता का अक्ष कहा जाता है। उदाहरण के लिए, अंतरिक्ष में एक सपाट आयत आकार सममित होता है और इसमें सममिति के 3 अक्ष होते हैं, यदि यह एक वर्ग नहीं है।

- घूर्णी समरूपता।

प्राकृतिक विज्ञान में, अक्षीय समरूपता को एक सीधी रेखा के चारों ओर घूमने के सापेक्ष घूर्णी समरूपता के रूप में समझा जाता है। इस मामले में, निकायों को अक्षीय सममित कहा जाता है यदि वे इस सीधी रेखा के चारों ओर किसी भी मोड़ पर स्वयं में परिवर्तित हो जाते हैं। इस मामले में, आयत एक अक्षीय निकाय नहीं होगा, लेकिन इसमें एक शंकु होगा।

हमारे चारों ओर दुनिया की कई वस्तुओं के समतल पर छवियों में समरूपता की धुरी या समरूपता का केंद्र होता है। कई पेड़ के पत्ते और फूलों की पंखुड़ियाँ मध्य तने के बारे में सममित होती हैं।

हम अक्सर कला, वास्तुकला, प्रौद्योगिकी और रोजमर्रा की जिंदगी में समरूपता का सामना करते हैं। कई इमारतों के अग्रभाग अक्षीय रूप से सममित हैं। ज्यादातर मामलों में, कालीन, कपड़े और कमरे के वॉलपेपर पर पैटर्न एक अक्ष या केंद्र के बारे में सममित होते हैं। तंत्र के कई भाग सममित होते हैं, जैसे गियर।

अक्षीय समरूपता। अक्षीय समरूपता के साथ, आकृति का प्रत्येक बिंदु उस बिंदु पर जाता है जो एक निश्चित रेखा के संबंध में सममित होता है।

प्रस्तुति "आभूषण" से चित्र 35"समरूपता" विषय पर ज्यामिति पाठों के लिए

आयाम: 360 x 260 पिक्सेल, प्रारूप: jpg। एक ज्यामिति पाठ के लिए एक चित्र मुफ्त में डाउनलोड करने के लिए, छवि पर राइट-क्लिक करें और "छवि को इस रूप में सहेजें ..." पर क्लिक करें। पाठ में चित्र दिखाने के लिए, आप संपूर्ण प्रस्तुति "Ornament.ppt" को ज़िप-संग्रह में सभी चित्रों के साथ निःशुल्क डाउनलोड कर सकते हैं। संग्रह का आकार 3324 केबी है।

प्रस्तुति डाउनलोड करें

समरूपता

"समरूपता का बिंदु" - केंद्रीय समरूपता। मैं एक 1. अक्षीय और केंद्रीय समरूपता। बिंदु C को सममिति का केंद्र कहा जाता है। रोजमर्रा की जिंदगी में समरूपता। गोल शंकु अक्षीय रूप से सममित है; समरूपता की धुरी शंकु की धुरी है। सममिति के दो से अधिक अक्षों वाली आकृतियाँ। समांतर चतुर्भुज में केवल केंद्रीय समरूपता होती है।

"गणितीय समरूपता" - समरूपता क्या है? शारीरिक समरूपता। जीव विज्ञान में समरूपता। समरूपता इतिहास। हालांकि, जटिल अणुओं में आमतौर पर समरूपता का अभाव होता है। पालिंड्रोम। समरूपता। एक्स और एम और में। गणित में अनुवाद समरूपता के साथ बहुत कुछ समान है। लेकिन वास्तव में, हम समरूपता के बिना कैसे रहेंगे? अक्षीय समरूपता।

"आभूषण" - बी) पट्टी पर। समानांतर अनुवाद केंद्रीय समरूपता अक्षीय समरूपता रोटेशन। रैखिक (लेआउट): केंद्रीय समरूपता और समानांतर अनुवाद का उपयोग करके एक आभूषण बनाता है। विमान। आभूषण की किस्मों में से एक जालीदार आभूषण है। आभूषण बनाने के लिए प्रयुक्त परिवर्तन:

"प्रकृति में समरूपता" - ज्यामितीय आकृतियों के मुख्य गुणों में से एक समरूपता है। विषय को संयोग से नहीं चुना गया था, क्योंकि अगले साल हमें एक नए विषय - ज्यामिति का अध्ययन शुरू करना होगा। वन्यजीवों में समरूपता की घटना प्राचीन ग्रीस में देखी गई थी। हम स्कूल वैज्ञानिक समुदाय में पढ़ते हैं क्योंकि हम कुछ नया और अज्ञात सीखना पसंद करते हैं।

"ज्यामिति में आंदोलन" - गणित सुंदर और सामंजस्यपूर्ण है! आंदोलन के कुछ उदाहरण क्या हैं? ज्यामिति में आंदोलन। आंदोलन किसे कहते हैं? आंदोलन किन विज्ञानों पर लागू होता है? मानव गतिविधि के विभिन्न क्षेत्रों में आंदोलन का उपयोग कैसे किया जाता है? सिद्धांतकारों का एक समूह। गति की अवधारणा अक्षीय समरूपता केंद्रीय समरूपता। क्या हम प्रकृति में गति देख सकते हैं?

कला में समरूपता - लेविटन। राफेल। द्वितीय 1. वास्तु में अनुपात। लय माधुर्य की अभिव्यक्ति के मुख्य तत्वों में से एक है। आर डेसकार्टेस। शिप ग्रोव। ए.वी. वोलोशिनोव। वेलास्केज़ "डिलीवरी डिलीरियम"। बाह्य रूप से, सद्भाव स्वयं को माधुर्य, लय, समरूपता, आनुपातिकता में प्रकट कर सकता है। II.4 साहित्य में अनुपात

कुल 32 प्रस्तुतियाँ हैं

अक्षीय समरूपता और पूर्णता की अवधारणा

अक्षीय समरूपता प्रकृति के सभी रूपों में निहित है और सुंदरता के मूलभूत सिद्धांतों में से एक है। मनुष्य ने प्राचीन काल से कोशिश की है

पूर्णता का अर्थ समझें। इस अवधारणा को सबसे पहले प्राचीन ग्रीस के कलाकारों, दार्शनिकों और गणितज्ञों ने प्रमाणित किया था। और "समरूपता" शब्द का आविष्कार उनके द्वारा ही किया गया था। यह संपूर्ण के भागों की आनुपातिकता, सद्भाव और पहचान को दर्शाता है। प्राचीन यूनानी विचारक प्लेटो ने तर्क दिया कि केवल सममित और आनुपातिक वस्तु ही सुंदर हो सकती है। वास्तव में, वे घटनाएं और रूप जिनमें आनुपातिकता और पूर्णता होती है, वे "आंख को प्रसन्न करने वाले" होते हैं। हम उन्हें सही कहते हैं।

एक अवधारणा के रूप में अक्षीय समरूपता

जीवों के संसार में समरूपता केंद्र या अक्ष के सापेक्ष शरीर के समान भागों की नियमित व्यवस्था में प्रकट होती है। अधिक बार

अक्षीय समरूपता प्रकृति में होती है। यह न केवल जीव की सामान्य संरचना को निर्धारित करता है, बल्कि इसके बाद के विकास की संभावनाओं को भी निर्धारित करता है। जीवित प्राणियों के ज्यामितीय आकार और अनुपात "अक्षीय समरूपता" द्वारा बनते हैं। इसकी परिभाषा इस प्रकार तैयार की गई है: यह विभिन्न परिवर्तनों के तहत संयुक्त होने वाली वस्तुओं की संपत्ति है। पूर्वजों का मानना ​​​​था कि गोले में पूरी तरह से समरूपता का सिद्धांत है। वे इस रूप को सामंजस्यपूर्ण और परिपूर्ण मानते थे।

वन्य जीवन में अक्षीय समरूपता

यदि आप किसी भी जीवित प्राणी को देखें, तो जीव की संरचना की समरूपता तुरंत हड़ताली है। मनुष्य: दो हाथ, दो पैर, दो आंखें, दो कान, इत्यादि। प्रत्येक प्रकार के जानवर का एक विशिष्ट रंग होता है। यदि रंग में एक चित्र दिखाई देता है, तो, एक नियम के रूप में, यह दोनों तरफ प्रतिबिंबित होता है। इसका मतलब है कि एक निश्चित रेखा है जिसके साथ जानवरों और लोगों को नेत्रहीन रूप से दो समान हिस्सों में विभाजित किया जा सकता है, अर्थात उनकी ज्यामितीय संरचना अक्षीय समरूपता पर आधारित है। प्रकृति किसी भी जीवित जीव को अराजक और संवेदनहीन रूप से नहीं, बल्कि विश्व व्यवस्था के सामान्य नियमों के अनुसार बनाती है, क्योंकि ब्रह्मांड में कुछ भी विशुद्ध रूप से सौंदर्यपूर्ण, सजावटी उद्देश्य नहीं है। विभिन्न रूपों की उपस्थिति भी एक प्राकृतिक आवश्यकता के कारण होती है।

निर्जीव प्रकृति में अक्षीय समरूपता

दुनिया में हम हर जगह ऐसी घटनाओं और वस्तुओं से घिरे हैं जैसे: आंधी, इंद्रधनुष, बूंद, पत्ते, फूल, आदि। उनका दर्पण, रेडियल, केंद्रीय, अक्षीय समरूपता स्पष्ट है। यह काफी हद तक गुरुत्वाकर्षण की घटना के कारण है। अक्सर समरूपता की अवधारणा को किसी भी घटना के परिवर्तन की नियमितता के रूप में समझा जाता है: दिन और रात, सर्दी, वसंत, गर्मी और शरद ऋतु, और इसी तरह। व्यवहार में, यह गुण वहाँ मौजूद है जहाँ भी आदेश देखा जाता है। और प्रकृति के नियम स्वयं - जैविक, रासायनिक, आनुवंशिक, खगोलीय, हम सभी के लिए सामान्य समरूपता के सिद्धांतों के अधीन हैं, क्योंकि उनमें एक गहरी स्थिरता है। इस प्रकार, संतुलन, एक सिद्धांत के रूप में पहचान का एक सार्वभौमिक पैमाना है। प्रकृति में अक्षीय समरूपता "आधारशिला" कानूनों में से एक है जिस पर संपूर्ण ब्रह्मांड आधारित है।

वैज्ञानिक और व्यावहारिक सम्मेलन

समझौता ज्ञापन "माध्यमिक विद्यालय संख्या 23"

वोलोग्डा शहर

खंड: प्राकृतिक - वैज्ञानिक

डिजाइन और अनुसंधान कार्य

समरूपता प्रकार

कक्षा 8 "ए" के छात्र का काम पूरा किया

क्रेनेवा मार्गारीटा

पर्यवेक्षक: उच्च गणित शिक्षक

वर्ष 2014

परियोजना संरचना:

1 परिचय।

2. परियोजना के लक्ष्य और उद्देश्य।

3. समरूपता के प्रकार:

3.1. केंद्रीय समरूपता;

3.2. अक्षीय समरूपता;

3.3. मिरर समरूपता (विमान के बारे में समरूपता);

3.4. घूर्णी समरूपता;

3.5. पोर्टेबल समरूपता।

4 निर्णय।

समरूपता वह विचार है जिसके माध्यम से मनुष्य ने सदियों से व्यवस्था, सौंदर्य और पूर्णता को समझने और बनाने का प्रयास किया है।

जी. वेइला

परिचय।

मेरे काम का विषय "8 वीं कक्षा की ज्यामिति" पाठ्यक्रम में "अक्षीय और केंद्रीय समरूपता" खंड का अध्ययन करने के बाद चुना गया था। मुझे इस विषय में बहुत दिलचस्पी थी। मैं जानना चाहता था: किस प्रकार की समरूपता मौजूद है, वे एक दूसरे से कैसे भिन्न हैं, प्रत्येक प्रकार में सममित आकृतियों के निर्माण के सिद्धांत क्या हैं।

काम का उद्देश्य : विभिन्न प्रकार की समरूपता का परिचय।

कार्य:

इस मुद्दे पर साहित्य का अध्ययन करें।

अध्ययन की गई सामग्री को सारांशित और व्यवस्थित करें।

एक प्रस्तुति तैयार करें।

प्राचीन काल में "सद्भाव", "सौंदर्य" के अर्थ में "SYMMETRY" शब्द का प्रयोग किया जाता था। ग्रीक से अनुवादित, इस शब्द का अर्थ है "आनुपातिकता, आनुपातिकता, किसी बिंदु, सीधी रेखा या तल के विपरीत पक्षों पर किसी चीज़ के भागों की व्यवस्था में समानता।

समरूपता के दो समूह हैं।

पहले समूह में पदों, रूपों, संरचनाओं की समरूपता शामिल है। यह वह समरूपता है जिसे आप सीधे देख सकते हैं। इसे ज्यामितीय समरूपता कहा जा सकता है।

दूसरा समूह भौतिक घटनाओं और प्रकृति के नियमों की समरूपता की विशेषता है। यह समरूपता दुनिया की प्राकृतिक-वैज्ञानिक तस्वीर की नींव पर है: इसे भौतिक समरूपता कहा जा सकता है।

मैं पढ़ाई पर ध्यान दूंगाज्यामितीय समरूपता .

बदले में, कई प्रकार के ज्यामितीय समरूपता भी हैं: केंद्रीय, अक्षीय, दर्पण (विमान के सापेक्ष समरूपता), रेडियल (या रोटरी), पोर्टेबल, और अन्य। मैं आज 5 प्रकार की समरूपता देखूंगा।

केंद्रीय समरूपता

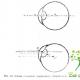
दो बिंदु A और A 1 बिंदु O के संबंध में सममित कहलाते हैं यदि वे m O से गुजरने वाली एक सीधी रेखा पर स्थित हैं और समान दूरी पर इसके विपरीत दिशा में स्थित हैं। बिंदु O को सममिति का केंद्र कहा जाता है।

आकृति को एक बिंदु के बारे में सममित कहा जाता है।हे यदि आकृति के प्रत्येक बिंदु के लिए बिंदु के सापेक्ष एक बिंदु सममित हैहे भी इस आंकड़े के अंतर्गत आता है। बिंदुहे आकृति की सममिति का केंद्र कहा जाता है, आकृति को केंद्रीय सममिति कहा जाता है।

केंद्रीय समरूपता वाली आकृतियों के उदाहरण एक वृत्त और एक समांतर चतुर्भुज हैं।

स्लाइड पर दिखाए गए आंकड़े किसी बिंदु के बारे में सममित हैं

2. अक्षीय समरूपता

दो बिंदुएक्स तथा यू सीधी रेखा के संबंध में सममित कहलाते हैंटी , यदि यह सीधी रेखा खंड XY के मध्य से होकर गुजरती है और उस पर लंबवत है। यह भी कहा जाना चाहिए कि सीधी रेखा का प्रत्येक बिंदुटी अपने आप में सममित माना जाता है।

सीधाटी - समरूपता की धुरी।

एक सीधी रेखा के परितः सममित आकृति कहलाती है।टी, यदि आकृति के प्रत्येक बिंदु के लिए एक सीधी रेखा के सापेक्ष एक सममित बिंदु हैटी भी इस आंकड़े के अंतर्गत आता है।

सीधाटीआकृति की सममिति की धुरी कहलाती है, वे कहते हैं कि आकृति में अक्षीय सममिति है।

अक्षीय समरूपता में एक अविकसित कोण, समद्विबाहु और समबाहु त्रिभुज, एक आयत और एक समचतुर्भुज होता है,पत्र (प्रस्तुति देखें)।

मिरर समरूपता (एक विमान के बारे में समरूपता)

दो अंक पी 1 तथा P को समतल के बारे में सममित कहा जाता है और यदि वे समतल a के लंबवत सीधी रेखा पर स्थित हैं, और इससे समान दूरी पर हैं

मिरर समरूपता हर व्यक्ति को अच्छी तरह से जाना जाता है। यह किसी भी वस्तु और उसके प्रतिबिंब को समतल दर्पण में जोड़ता है। वे कहते हैं कि एक आकृति दूसरे के प्रति दर्पण-सममित होती है।

समतल पर, समरूपता के अनगिनत अक्षों वाली आकृति एक वृत्त थी। अंतरिक्ष में, समरूपता के अनंत विमानों में एक गेंद होती है।

लेकिन अगर सर्कल एक तरह का है, तो त्रि-आयामी दुनिया में समरूपता के अनंत संख्या में निकायों की एक पूरी श्रृंखला होती है: आधार पर एक सर्कल के साथ एक सीधा सिलेंडर, एक गोलाकार आधार वाला शंकु, एक गेंद।

यह स्थापित करना आसान है कि प्रत्येक सममित सपाट आकृति को दर्पण का उपयोग करके स्वयं के साथ संरेखित किया जा सकता है। यह आश्चर्य की बात है कि पाँच-नुकीले तारे या एक समबाहु पंचभुज जैसी जटिल आकृतियाँ भी सममित होती हैं। जैसा कि यह कुल्हाड़ियों की संख्या से होता है, वे अपनी उच्च समरूपता द्वारा ठीक से प्रतिष्ठित होते हैं। और इसके विपरीत: यह समझना इतना आसान नहीं है कि तिरछे समांतर चतुर्भुज के रूप में ऐसा प्रतीत होने वाला सही आंकड़ा विषम क्यों है।

4. पी घूर्णी समरूपता (या रेडियल समरूपता)

घूर्णी समरूपता - यह समरूपता है, वस्तु का आकार संरक्षित है360 ° / के बराबर कोण पर एक निश्चित अक्ष के चारों ओर घूमते समयएन(या इस मान का गुणज), जहाँएन= 2, 3, 4, ... निर्दिष्ट अक्ष को घूर्णन अक्ष कहा जाता हैएनवें क्रम।

परn = 2 आकृति के सभी बिंदुओं को 180 . के कोण पर घुमाया जाता है 0 ( 360 0 /2 = 180 0 ) अक्ष के चारों ओर, जबकि आकृति का आकार संरक्षित है, अर्थात। एक आकृति का प्रत्येक बिंदु एक ही आकार के एक बिंदु पर जाता है (आकृति अपने आप बदल जाती है)। अक्ष को द्वितीय कोटि की धुरी कहा जाता है।

चित्रा 2 चित्रा 3 - 4 वें क्रम में, चित्रा 4 - 5 वें क्रम में तीसरे क्रम की धुरी दिखाता है।

एक वस्तु में एक से अधिक धुरी अक्ष हो सकते हैं: अंजीर। 1 - 3 धुरी कुल्हाड़ियों, अंजीर। 2 - 4 कुल्हाड़ियों, अंजीर। 3 - 5 कुल्हाड़ियों, अंजीर। 4 - केवल 1 अक्ष

प्रसिद्ध अक्षरों "I" और "F" में घूर्णी समरूपता है। दूसरे शब्दों में, अक्षर "I" लगभग 180 ° रोटेशन, 180 ° = 360 °: 2, सममित है।एन= 2, इसलिए इसमें द्वितीय कोटि की सममिति है।

ध्यान दें कि अक्षर "Ф" में दूसरे क्रम की घूर्णी समरूपता भी है।

इसके अलावा, अक्षर और समरूपता का केंद्र है, और अक्षर F में समरूपता का अक्ष है

आइए वास्तविक जीवन के उदाहरणों पर वापस जाएं: एक गिलास, एक शंकु के आकार का आइसक्रीम का पाउंड, तार का एक टुकड़ा, एक पाइप।

यदि हम इन पिंडों पर करीब से नज़र डालें, तो हम देखेंगे कि ये सभी, एक तरह से या किसी अन्य, समरूपता के अक्षों के अनंत सेट के माध्यम से एक वृत्त से मिलकर बने होते हैं, जिनमें से अनंत संख्या में समरूपता के विमान गुजरते हैं। इनमें से अधिकांश निकायों (उन्हें क्रांति के निकाय कहा जाता है) में, निश्चित रूप से, समरूपता का केंद्र (एक वृत्त का केंद्र) होता है, जिसके माध्यम से समरूपता का कम से कम एक रोटरी अक्ष गुजरता है।

यह स्पष्ट रूप से दिखाई देता है, उदाहरण के लिए, आइसक्रीम के साथ पाउंड के शंकु पर अक्ष। यह सर्कल के बीच से (आइसक्रीम से बाहर चिपके हुए!) फंकी कोन के नुकीले सिरे तक चलता है। हम किसी पिंड के सममिति तत्वों की समग्रता को एक प्रकार की सममिति माप के रूप में देखते हैं। गेंद, निस्संदेह, समरूपता के संदर्भ में, पूर्णता का एक नायाब अवतार है, एक आदर्श है। प्राचीन यूनानियों ने उन्हें सबसे उत्तम शरीर के रूप में माना, और चक्र, स्वाभाविक रूप से, सबसे उत्तम सपाट आकृति के रूप में।

किसी विशेष वस्तु की समरूपता का वर्णन करने के लिए, सभी घूर्णन अक्षों और उनके क्रम के साथ-साथ समरूपता के सभी विमानों को इंगित करना आवश्यक है।

उदाहरण के लिए, दो समान नियमित चतुर्भुज पिरामिडों से बना एक ज्यामितीय निकाय पर विचार करें।

इसमें एक चौथा क्रम रोटरी अक्ष (एबी अक्ष), चार द्वितीय क्रम रोटरी अक्ष (सीई अक्ष,डीएफ, एमपी, एनक्यू), समरूपता के पाँच तल (तल)सीडीईएफ, एएफबीडी, एसीबीई, एएमबीपी, एएनबीक्यू).

5 . पोर्टेबल समरूपता

एक अन्य प्रकार की सममिति हैपोर्टेबल साथ विषमता।

इस तरह की समरूपता की बात तब की जाती है, जब किसी आकृति को एक सीधी रेखा के साथ कुछ दूरी "a" या इस मान के गुणज के लिए एक दूरी पर ले जाने पर, यह स्वयं के साथ संयुक्त हो जाती है जिस सीधी रेखा के साथ स्थानांतरण किया जाता है उसे स्थानांतरण अक्ष कहा जाता है, और दूरी "ए" को प्राथमिक स्थानांतरण, अवधि या समरूपता का चरण कहा जाता है।

ए

एक लंबे रिबन पर समय-समय पर दोहराए जाने वाले पैटर्न को बॉर्डर कहा जाता है। व्यवहार में, सीमाएं विभिन्न रूपों (भित्तिचित्र, कच्चा लोहा, प्लास्टर बेस-रिलीफ या सिरेमिक) में पाई जाती हैं। एक कमरे को सजाते समय चित्रकारों और कलाकारों द्वारा सीमाओं का उपयोग किया जाता है। इन गहनों को पूरा करने के लिए एक स्टैंसिल बनाई जाती है। हम स्टैंसिल को घुमाते हैं, इसे पलटते हैं या इसे बिना मोड़े, समोच्च के चारों ओर खींचते हैं, ड्राइंग को दोहराते हैं, और एक आभूषण प्राप्त होता है (दृश्य प्रदर्शन)।

बॉर्डर को आसानी से एक स्टैंसिल (मूल तत्व) का उपयोग करके बनाया जा सकता है, इसे स्लाइड या फ़्लिप करके और पैटर्न को दोहराते हुए। आंकड़ा पांच प्रकार के स्टेंसिल दिखाता है:ए ) विषम;बी, सी ) समरूपता का एक अक्ष होना: क्षैतिज या लंबवत;जी ) केंद्रीय सममित;डी ) समरूपता के दो अक्ष हैं: लंबवत और क्षैतिज।

निम्नलिखित परिवर्तनों का उपयोग कर्ब बनाने के लिए किया जाता है:

ए ) समानांतर स्थानांतरण;बी ) ऊर्ध्वाधर अक्ष के बारे में समरूपता;वी ) केंद्रीय समरूपता;जी ) क्षैतिज अक्ष के बारे में समरूपता।

इसी तरह, आप सॉकेट बना सकते हैं। ऐसा करने के लिए, सर्कल को विभाजित किया गया हैएन समान क्षेत्र, उनमें से एक में पैटर्न का एक नमूना किया जाता है और फिर बाद वाले को सर्कल के शेष हिस्सों में क्रमिक रूप से दोहराया जाता है, हर बार पैटर्न को 360 ° / के कोण के माध्यम से घुमाते हैं।एन .

अक्षीय और पोर्टेबल समरूपता के आवेदन का एक अच्छा उदाहरण तस्वीर में दिखाया गया बाड़ है।

निष्कर्ष: इस प्रकार, विभिन्न प्रकार की समरूपता होती है, इनमें से प्रत्येक प्रकार की सममिति में सममित बिंदु कुछ नियमों के अनुसार निर्मित होते हैं। जीवन में, हम हर जगह किसी न किसी रूप में समरूपता में मिलते हैं, और अक्सर हमारे आस-पास की वस्तुओं में, कई प्रकार की समरूपता एक साथ नोट की जा सकती है। यह हमारे आसपास की दुनिया में व्यवस्था, सुंदरता और पूर्णता पैदा करता है।

साहित्य:

प्रारंभिक गणित की हैंडबुक। एम. हां. वायगोडस्की। - प्रकाशन गृह "विज्ञान"। - मास्को 1971। - 416पी.

विदेशी शब्दों का आधुनिक शब्दकोश। - एम।: रूसी भाषा, 1993.

स्कूल में गणित का इतिहासनौवीं - एक्सकक्षाएं। जी.आई. ग्लेज़र। - प्रकाशन गृह "शिक्षा"। - मास्को 1983। - 351पी।

दृश्य ज्यामिति 5 - 6 ग्रेड। अगर। शेरगिन, एल.एन. एर्गांज़िवा। - पब्लिशिंग हाउस "ड्रोफा", मॉस्को 2005। - 189पी.

बच्चों के लिए विश्वकोश। जीव विज्ञान। एस इस्माइलोवा। - पब्लिशिंग हाउस "अवंता +"। - मास्को 1997। - 704पी.

उर्मंतसेव यू.ए. प्रकृति की समरूपता और समरूपता की प्रकृति - एम।: विचार arxitecht / अर्हकोम्प2. एचटीएम, , ru.wikipedia.org/wiki/