चर प्रतिस्थापन विधि का उपयोग करके द्विघात समीकरण को कैसे हल करें। प्रतिस्थापन का उपयोग करके समीकरणों को हल करना

परिचय

गणित की शिक्षा एक समग्र विद्यालय में प्राप्त होती है आवश्यक घटक सामान्य शिक्षाऔर सामान्य संस्कृति आधुनिक आदमी. आधुनिक मनुष्य को घेरने वाली लगभग हर चीज़ किसी न किसी तरह गणित से जुड़ी हुई है। और भौतिकी, इंजीनियरिंग और सूचना प्रौद्योगिकी में हालिया प्रगति से इसमें कोई संदेह नहीं रह गया है कि भविष्य में भी स्थिति वैसी ही रहेगी। इसलिए, कई व्यावहारिक समस्याओं का समाधान समाधान तक ही सीमित रहता है विभिन्न प्रकारसमीकरण जिन्हें हल करना आपको सीखना होगा।

प्रारंभिक गणित में, दो प्रकार के समीकरण होते हैं: बीजगणितीय और पारलौकिक समीकरण शामिल हैं:

रैखिक; वर्ग; घन; द्विघात; सामान्य रूप की चौथी डिग्री का समीकरण;द्विपद बीजीय

समीकरण nवें डिग्री; शक्ति बीजगणितीय; – रिफ्लेक्सिव (बीजगणितीय); - सामान्य रूप की वें डिग्री का बीजगणितीय समीकरण; 10. भिन्नात्मक बीजगणितीय समीकरण, अर्थात्। बहुपद वाले समीकरण और

बीजीय भिन्न

11. (फॉर्म के अंश, कहाँ और बहुपद हैं);

तर्कहीन समीकरण

, यानी मूलांक वाले समीकरण, जिसके अंतर्गत बहुपद और बीजगणितीय भिन्न होते हैं; 12. एक मापांक वाले समीकरण, जिसके मापांक के अंतर्गत बहुपद और बीजगणितीय भिन्न समाहित होते हैं।लघुगणक, घातांक, या जैसे पारलौकिक कार्यों वाले समीकरण

त्रिकोणमितीय फलन

, पारलौकिक कहलाते हैं। अपने कार्य में हम बीजगणितीय समीकरणों पर अधिक विस्तार से विचार करेंगे।

शैक्षिक और कार्यप्रणाली साहित्य परंपरागत रूप से समीकरणों को हल करने के लिए विशेष तकनीकों पर चर्चा करता है। इस बीच, प्रत्येक अनुभाग के समीकरणों को हल करने की विशिष्टता एक गौण मामला है। मूलतः चार मुख्य विधियाँ हैं:

समीकरण h (f(x))=h (g(x)) को समीकरण f(x)=g(x) से बदलना;

परिवर्तनीय प्रतिस्थापन विधि;

गुणनखंडन विधि;

कार्यात्मक-ग्राफिक विधि और उनके विभिन्न संशोधन। उनमें से सबसे आम परिवर्तनीय प्रतिस्थापन विधि है।इसके आधार पर, हम अपने काम का लक्ष्य बनाते हैं: हल करते समय अज्ञात को प्रतिस्थापित करने की विधि की संभावनाओं का अध्ययन करना बीजगणितीय समीकरणऔर मानक और में उनके अनुप्रयोग को प्रदर्शित करें

1. समीकरणों को हल करने के सिद्धांत से संबंधित बुनियादी अवधारणाओं और कथनों की सामग्री को प्रकट करें: समीकरण को हल करना, तुल्यता और परिणाम, समीकरणों को हल करने के सामान्य तरीके।

2. मानक और गैर-मानक स्थितियों में बीजगणितीय समीकरणों को हल करते समय अज्ञात को प्रतिस्थापित करने की विधि का उपयोग करने की संभावनाओं की पहचान करें।

3. बीजगणितीय समीकरणों को हल करते समय नए अज्ञात को पेश करने के तरीकों को टाइप करना और उनकी प्रयोज्यता के मानदंडों की पहचान करना

4. एक किट बनाएं विशिष्ट कार्य, जो समीकरणों को हल करते समय प्रतिस्थापन विधि के उपयोग को कम करता है, और उनके समाधान को प्रदर्शित करता है।

1. समीकरणों को हल करने के सिद्धांत से संबंधित बुनियादी अवधारणाएँ और कथन

अपने काम के पहले अध्याय में, हम समीकरणों को हल करने के सिद्धांत से संबंधित बुनियादी अवधारणाओं और कथनों की सामग्री को प्रकट करेंगे।

हम गणित के पाठों में पहले से ही "समीकरण" की अवधारणा से परिचित हो गए हैं प्राथमिक स्कूल, और "एक समीकरण को हल करें" समस्या संभवतः सबसे अधिक बार सामने आने वाली समस्या है। हालाँकि, दे दो सटीक परिभाषा"समीकरण" की अवधारणा, हम प्रारंभिक गणित में पाठ्यक्रम के दायरे से परे जाने के बिना सटीक रूप से यह परिभाषित नहीं कर सकते कि "समीकरण को हल करने" का क्या अर्थ है। ऐसा करने के लिए, बहुत गंभीर तार्किक और यहाँ तक कि दार्शनिक श्रेणियों को भी शामिल करना आवश्यक है। "सामान्य ज्ञान" के स्तर पर इन अवधारणाओं से परिचित होना हमारे लिए काफी है।

समान अज्ञात वाले दो समीकरण A और B पर विचार करें। हम कहेंगे कि समीकरण B है परिणामसमीकरण A यदि समीकरण A का कोई भी मूल समीकरण B का मूल है।

समीकरण कहलाते हैं समकक्ष,यदि उनमें से एक की कोई जड़ दूसरे की जड़ है और इसके विपरीत। इस प्रकार, समीकरण समतुल्य हैं यदि उनमें से प्रत्येक दूसरे का परिणाम है।

उदाहरण के लिए, इन परिभाषाओं से यह पता चलता है कि जिन दो समीकरणों का कोई समाधान नहीं है वे समतुल्य हैं। यदि A के पास कोई समाधान नहीं है, तो B के पास है परिणामए, समीकरण बी जो भी हो।

आइए हम "समीकरण को हल करने" की अवधारणा को परिभाषित करें। प्रश्न हल करें- का अर्थ है इसमें शामिल अज्ञात के सभी मूल्यों को ढूंढना जो समीकरण को एक पहचान में बदल देते हैं। इन मानों को समीकरण के मूल कहा जाता है।

समीकरणों को हल करने की प्रक्रिया में मुख्य रूप से किसी दिए गए समीकरण को उसके समकक्ष दूसरे समीकरण से बदलना शामिल है।

जैसा कि पहले उल्लेख किया गया है, सबसे अधिक चार हैं सामान्य तरीके, किसी भी प्रकार के समीकरणों को हल करने में उपयोग किया जाता है। आइए प्रत्येक विधि पर करीब से नज़र डालें।

समीकरण h (f(x))=h (g(x)) को समीकरण f(x)=g(x) से बदलने की विधि का उपयोग केवल तभी किया जा सकता है जब

- एक मोनोटोनिक फ़ंक्शन जो प्रत्येक मान को एक बार लेता है। यदि यह फ़ंक्शन गैर-मोनोटोनिक है, तो इस विधि का उपयोग नहीं किया जा सकता है, क्योंकि जड़ों का नुकसान संभव है।

गुणनखंडन विधि का सार इस प्रकार है: समीकरण

प्रतिस्थापित किया जा सकता है:

इस सेट के समीकरणों को हल करने के बाद, आपको उन जड़ों को लेना होगा जो मूल समीकरण की परिभाषा के क्षेत्र से संबंधित हैं, और बाकी को बाहरी विचार के रूप में त्याग दें ग्राफ़िक विधिसमीकरण का समाधान

क्या यह है: आपको फ़ंक्शंस के ग्राफ़ बनाने और उनके प्रतिच्छेदन बिंदु ढूंढने की आवश्यकता है। समीकरण की जड़ें इन बिंदुओं के भुज हैं। यह विधि आपको किसी समीकरण के मूलों की संख्या निर्धारित करने, मूल के मान का अनुमान लगाने, मूलों के अनुमानित और कभी-कभी सटीक मान ज्ञात करने की अनुमति देती है। कुछ मामलों में, फ़ंक्शंस के ग्राफ़ के निर्माण को फ़ंक्शंस के कुछ गुणों के संदर्भ द्वारा प्रतिस्थापित किया जा सकता है (यही कारण है कि हम ग्राफिकल के बारे में नहीं, बल्कि समीकरणों को हल करने के लिए एक कार्यात्मक-ग्राफ़िकल विधि के बारे में बात कर रहे हैं)। यदि, उदाहरण के लिए, कार्यों में से एक बढ़ता है, और दूसरा घटता है, तो समीकरण की या तो कोई जड़ नहीं होती है या उसकी एक जड़ होती है आइए कार्यात्मक-ग्राफ़िकल विधि की एक और सुंदर विविधता का उल्लेख करें: यदि अंतराल पर उच्चतम मूल्यकार्यों में से एक, बराबर और सबसे छोटा मूल्यएक अन्य फ़ंक्शन भी के बराबर है, तो समीकरण अंतराल पर समीकरणों की एक प्रणाली के बराबर है।

आइए हम चर प्रतिस्थापन विधि का सार प्रकट करें: यदि समीकरण

विषय पर पाठ और प्रस्तुति: "परिवर्तनीय प्रतिस्थापन विधि। उदाहरण"

अतिरिक्त सामग्री
प्रिय उपयोगकर्ताओं, अपनी टिप्पणियाँ, समीक्षाएँ, शुभकामनाएँ छोड़ना न भूलें! सभी सामग्रियों की जांच एंटी-वायरस प्रोग्राम द्वारा की गई है।

ग्रेड 11 के लिए इंटीग्रल ऑनलाइन स्टोर में शिक्षण सहायक सामग्री और सिमुलेटर
1सी: स्कूल। ज्यामिति में समस्याओं का समाधान. ग्रेड 10-11 के लिए अंतरिक्ष में निर्माण पर इंटरैक्टिव कार्य
मापदंडों के साथ बीजगणितीय समस्याएं, ग्रेड 9-11

समीकरणों को हल करते समय यह विधि काफी सामान्य है, और हमने इसे एक से अधिक बार उपयोग किया है, इसका उपयोग निम्नलिखित मामलों में किया जा सकता है:

• यदि मूल समीकरण $f(x)=0$ है जटिल रूप, लेकिन इसे $h(g(x))=0$ के रूप के समीकरण में बदलना संभव था।
• वेरिएबल $u=g(x)$ में परिवर्तन करना आवश्यक है।
• समीकरण $h(u)=0$ को हल करें, मूल खोजें $u_1$, $u_2$, … $u_n$।
• विपरीत प्रतिस्थापन $g(x)=u_1$, $g(x)=u_2$, … , $g(x)=u_n$ दर्ज करें।
• प्रत्येक समीकरण को हल करें $g(x)=u_1$, $g(x)=u_2$, …, $g(x)=u_n$. प्रत्येक समीकरण के मूल मूल समीकरण के समाधान होंगे।

चर प्रतिस्थापन विधि के लिए समीकरणों के साथ काम करने में अच्छे कौशल और अनुभव की आवश्यकता होती है। फैसले के बाद बड़ी मात्रासमीकरण सामान्य रूप से देखेंइन समीकरणों को अच्छी तरह से याद किया जाता है और ऐसे प्रतिस्थापन के साथ आना बहुत आसान हो जाता है जो पहले से ही ज्ञात समीकरणों की ओर ले जाता है। समीकरणों को प्रतिस्थापित करते समय प्राप्त सभी मूलों की जांच करना और उसके बाद ही मूल चर पर लौटना भी उचित है।

उदाहरण।
समीकरण हल करें: $8x^6+7x^3-1=0$.

समाधान।
आइए प्रतिस्थापन $y=x^3$ का परिचय दें। तब हमारा समीकरण एक द्विघात समीकरण में बदल जाता है:
$8y^2+7y-1=0$,
$(8y-1)(y+1)=0$,
$y_1=\frac(1)(8)$ और $y_2=-1$.

इस स्तर पर, अधिक निर्णय लेते समय जटिल समीकरणआपको प्राप्त जड़ों की जांच करनी चाहिए।
आइए विपरीत प्रतिस्थापन का परिचय दें: $x^3=\frac(1)(8)$ और $x^3=-1$।
इन समीकरणों की जड़ें ढूंढना आसान है: $x_1=\frac(1)(2)$ और $x_2=-1$।

उत्तर: $x=0.5$ और $x=-1$।

उदाहरण।
समीकरण हल करें: $\sqrt(\frac(2x+3)(2x-1))+4\sqrt(\frac(2x-1)(2x+3))=4$.

समाधान।
आइए समतुल्य परिवर्तन करें:
$\sqrt(\frac(2x-1)(2x+3))=(\frac(2x-1)(2x+3))^(\frac(1)(2))=(\frac(2x+ 3) )(2x-1))^(-\frac(1)(2))=((\frac(2x+3)(2x-1))^(\frac(1)(2)))^( - 1)=\frac(1)(\sqrt(\frac(2x+3)(2x-1)))$.

आइए प्रतिस्थापन का परिचय दें: $u=\sqrt(\frac(2x+3)(2x-1))$, फिर हमारा समीकरण कम होकर $u+\frac(4)(u)=4$ हो जाता है। $u^2-4u+4=0$, जहां से $u=2$.

आइए उलटा परिवर्तन प्रस्तुत करें: $\sqrt(\frac(2x+3)(2x-1))=2$।

$2x+3=4(2x-1)$, हल करना रैखिक समीकरण$x=1\frac(1)(6)$.

उदाहरण।
समीकरण हल करें: $2^x+2^(1-x)=3$.

समाधान।
हमारा समीकरण समतुल्य समीकरण में बदल जाता है: $2^x+\frac(2)(2^x)=3$.

आइए प्रतिस्थापन का परिचय दें: $t=2^x$।
$t+\frac(2)(t)=3$,
$t^2-3t+2=0$,
$(t-2)(t-1)=0$,
$t_1=2$ और $t_2=1$.

आइए विपरीत प्रतिस्थापन का परिचय दें: $2^x=2$ और $2^x=1$। प्रेषक: $x=1$ और $x=0$।

उत्तर: $x=1$ और $x=0$।

उदाहरण।
समीकरण हल करें: $lg^2(x^2)+lg(10x)-6=0$.

समाधान।
आइए अपने समीकरण को बदलें।
$lg^2(x^2)=(lg(x^2))^2=(2lg(x))^2=4lg^2x$.
$lg(10x)=lg10+lgx=1+lgx$.

मूल समीकरण समीकरण के समतुल्य है: $4lg^2x+lgx-5=0$.

आइए प्रतिस्थापन का परिचय दें: $u=lg(x)$।
$4u^2+u-5=0$,
$(4u+5)(u-1)=0$.

आइए विपरीत प्रतिस्थापन का परिचय दें: $lgx=-1.25$ और $lgx=1$।
उत्तर: $x=10^(-\frac(5)(4))$ और $x=10$.

उदाहरण।
समीकरण हल करें: $sin(x)cos(x)-6sin(x)+6cos(x)+6=0$.

समाधान।
आइए प्रतिस्थापन का परिचय दें: $cos(x)-sin(x)=y$.

फिर: $(cos(x)-sin(x))^2=1-2sin(x)cos(x)$.
$sin(x)cos(x)=\frac(1-y^2)(2)$.

मूल समीकरण इसके बराबर है:
$\frac(1-y^2)(2)+6y+6=0$,
$1-y^2+12y+12=0$,
$y^2-12y-13=0$,
$(y-13)(y+1)=0$.

आइए व्युत्क्रम प्रतिस्थापन का परिचय दें: $cos(x)-sin(x)=13$ - यह स्पष्ट है कि कोई समाधान नहीं है, क्योंकि कोसाइन और साइन मापांक में एक से सीमित हैं।

$cos(x)-sin(x)=-1$ - समीकरण के दोनों पक्षों को $\frac(\sqrt(2))(2)$ से गुणा करें।
$\frac(\sqrt(2))(2)cos(x)-\frac(\sqrt(2))(2)sin(x)=-\frac(\sqrt(2))(2)$.
$sin(\frac(π)(4)-x)=-\frac(\sqrt(2))(2)$.
$\begin (मामले) \frac(π)(4)-x=-\frac(π)(4)+2πn, \\ \frac(π)(4)-x=-\frac(3π)(4 )+2πn. \end (मामले)$
$\begin (मामले) x=\frac(π)(2)+2πn, \\ x=π+2πn. \end (मामले)$

उत्तर: $x=\frac(π)(2)+2πn$ और $π+2πn$.

स्वतंत्र रूप से हल करने योग्य समस्याएं

निम्नलिखित समीकरणों को हल करें:
1. $x^8+3x^4-4=0$.

2. $\sqrt(\frac(5x-1)(x+3))+5\sqrt(\frac(x+3)(5x-1))=6$.

3. $5^x+5^(2x+1)=-4$.
4. $2cos^2(x)-7cos-4=0$.
5. $5sin(2x)-11sin(x)=11cos(x)-7$.

चर परिवर्तन विधि का उपयोग करके समीकरणों को हल करना

जीवन के अधिकांश कार्य

बीजगणितीय समीकरणों के रूप में हल किए जाते हैं:

उन्हें उनके सरलतम रूप में लाना।

एल.एन. टॉल्स्टॉय.

पाठ का उद्देश्य: व्यवस्थित करें शैक्षणिक गतिविधियांछात्रों को चर प्रतिस्थापन विधि द्वारा उच्च डिग्री के संपूर्ण समीकरणों को हल करने की विधियों में महारत हासिल करना; छात्रों को पारस्परिक और सममित समीकरणों को हल करने की अवधारणाओं और तकनीकों से परिचित कराना।

कार्य:शैक्षिक:प्रतिस्थापन विधि का उपयोग करने की क्षमता विकसित करना जारी रखें

समीकरणों को हल करते समय परिवर्तनशील; समीकरणों को हल करने के लिए समान विधि देखने की क्षमता विकसित करना अलग-अलग स्थितियाँ; राज्य के स्तर से अधिक स्तर पर गैर-मानक समस्याओं और बीजगणितीय समीकरणों को हल करने के तरीकों और तकनीकों का एक विचार तैयार करना शैक्षिक मानक;

विकासशील:छात्रों की सोच का विकास; स्मृति विकास; विकास

तर्कसम्मत सोच, अपने विचारों को स्पष्ट रूप से तैयार करने की क्षमता; छात्रों की कल्पना का विकास; मौखिक भाषण का विकास.

शैक्षिक:अवलोकन कौशल की शिक्षा; स्वच्छता की शिक्षा

बोर्ड पर और नोटबुक में नोट्स बनाते समय; व्यावहारिक कार्य करते समय स्वतंत्रता का पोषण करना।

पाठ प्रगति

संगठनात्मक क्षण.

ज्ञान का अद्यतनीकरण एवं व्यवस्थितकरण।

कार्य क्रमांक 1. क्रासवर्ड पहेली को हल करें। अपने उत्तर नाममात्र मामले में ही लिखें।

क्षैतिज:

4.द्विघात समीकरण का व्यंजक क्या है? (विभेदक)

6. चर का वह मान जिस पर समीकरण वास्तविक समानता में बदल जाता है। (जड़)

8.रूप का समीकरण
, कहाँ
. (द्विघात)

9.द्विघात समीकरणों से संबंधित फ्रांसीसी गणितज्ञ। (वियतनाम)

10. एक समीकरण जिसमें बाएँ और दाएँ पक्ष पूर्णांक व्यंजक हैं। (साबुत)

11. एक चर वाले समीकरण जिनके मूलों का समूह समान हो। (समकक्ष)

खड़ा:

1. समीकरण की अनेक जड़ें. (समाधान)

2. समीकरण का हल
. (शून्य)

3. चर युक्त समानता। (समीकरण)

5. द्विघात समीकरण जिसमें गुणांक b या c में से एक 0 के बराबर है। (अपूर्ण)

7. द्विघात समीकरण जिसमें प्रथम गुणांक एक के बराबर. (दिया गया)

आज हम अपना पाठ किसको समर्पित करेंगे? (समीकरण हल करना )

कार्य क्रमांक 2. आप प्रत्येक समूह के समीकरणों को कैसे हल करेंगे?

उत्तर:समूह 1) के उदाहरणों को सामान्य गुणनखंड को कोष्ठक से बाहर रखकर या संक्षिप्त गुणन सूत्रों का उपयोग करके गुणनखंडन द्वारा सबसे अच्छा हल किया जाता है।

समूह 2) के उदाहरण समूहीकरण और गुणनखंडन द्वारा बेहतर ढंग से हल किए जाते हैं।

समूह 3) के उदाहरणों को एक नए चर का परिचय देकर और द्विघात समीकरण की ओर ले जाकर बेहतर ढंग से हल किया जा सकता है।

1 समूह 1 के उदाहरणों में आप कोष्ठक से कौन सा कारक निकालेंगे?

उत्तर:

आप समूह 2 उदाहरणों में शब्दों को किस प्रकार समूहित करेंगे?

उत्तर:

समूह 3 के उदाहरणों में नए चर से आपका क्या तात्पर्य है?

उत्तर:

आप एक बहुपद का गुणनखंड कैसे कर सकते हैं?
?

उत्तर: .

आज के पाठ में आप "चर प्रतिस्थापन विधि का उपयोग करके समीकरणों को हल करना" विषय पर अपना ज्ञान दिखाएंगे।

पाठ के विषय को अपनी नोटबुक में लिखें।

आज कक्षा में हम उच्च डिग्री के समीकरणों को हल करने के तरीकों में से एक पर गौर करेंगे - चर प्रतिस्थापन विधि; आइए व्युत्क्रम और सममित समीकरणों को हल करने की अवधारणाओं और तकनीकों से परिचित हों।

परिवर्तनीय प्रतिस्थापन करने की कला यह देखना है कि कौन सा प्रतिस्थापन सबसे अधिक सार्थक है और तेजी से सफलता की ओर ले जाता है।

कार्य क्रमांक 3.

प्रश्न हल करें।(2 छात्र एक ही समय में बोर्ड पर कार्य हल करते हैं।)

ए) (पहला छात्र स्पष्टीकरण के साथ बोर्ड पर हल करता है।)

बी) (दूसरा छात्र चुपचाप समीकरण हल करता है, फिर समाधान बताता है, कक्षा सुनती है और यदि कुछ स्पष्ट नहीं होता है तो प्रश्न पूछता है।)

1 छात्रप्रतिस्थापन:
.

2 छात्रप्रतिस्थापन:
.

(उन लोगों के लिए अतिरिक्त जिन्होंने पहले पिछले समीकरणों में महारत हासिल कर ली है)।

. .

3 छात्र

(छात्र सीट से समाधान की प्रगति पर टिप्पणी करते हैं।)

समाधान: आइए एक सामान्य कारक जोड़ें: ,

कहाँ
या
, यानी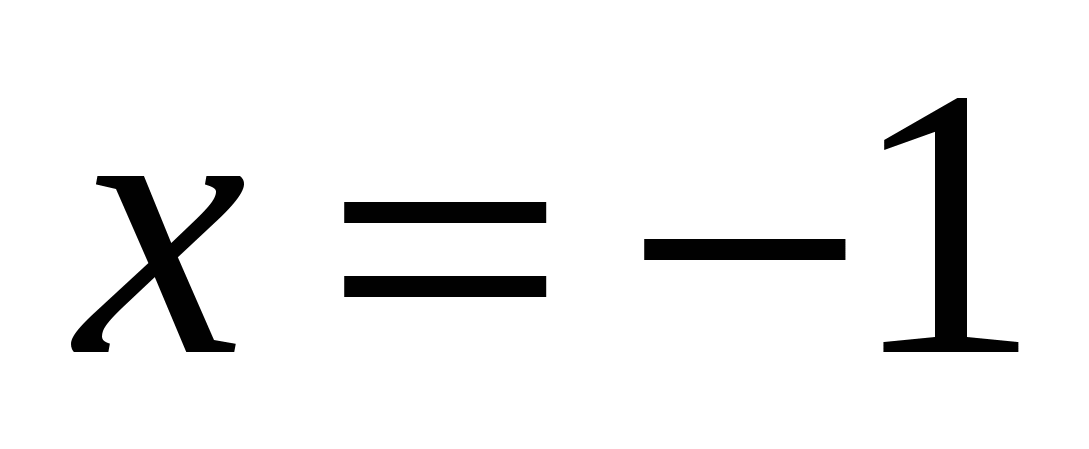

उत्तर:

ज्ञान को गहरा और विस्तारित करना

हम काम करना जारी रखते हैं। आप स्लाइड पर समीकरण देखें: x 4 -5x 3 +6x 2 -5x+1=0.

आप इसे कैसे हल करने का प्रस्ताव देंगे? काय करते?

क्या इसे भीतर ही सुलझाना संभव है स्कूल कार्यक्रमगणित में? उत्तर है नहीं. आख़िरकार मानक तरीकेस्कूल में समीकरणों को हल करने में दूसरी डिग्री से अधिक के समीकरणों को हल करना शामिल है। लेकिन हम याद कर सकते हैं कि व्यक्तिगत समीकरण अधिक हैं उच्च डिग्रीस्कूल में उन्होंने अभी भी निर्णय लिया। सच है, उन्हें हल करने के तरीके रचनात्मक अनुप्रयोग हैं ज्ञात विधियाँ, उन्हें दूसरे से अधिक डिग्री के एक या कई समीकरणों के समाधान में कम करना।

इस समीकरण को बहुत बारीकी से देखें? आपने क्या नोटिस किया? ?(इस समीकरण में सिरों से समान दूरी वाले गुणांक बराबर हैं)

दोस्तों, इस प्रकार का समीकरण, जब सिरों से समान दूरी पर स्थित गुणांक मेल खाते हैं, कहलाता है वापस करने. प्रतिस्थापन का उपयोग करके इस समीकरण को द्विघात समीकरण में घटाया जा सकता है।

मैं आपको उन्हें हल करने के लिए निम्नलिखित एल्गोरिदम प्रदान करता हूं:

पारस्परिक समीकरणों को हल करने के लिए एल्गोरिदम।

1. समीकरण के दोनों पक्षों को x 2 से विभाजित करें।

2.शब्दों को समूहित करें (पहला अंतिम के साथ, दूसरा चौथे के साथ)।

बनाने के लिए समीकरण कम करें ए + सी = 0

3.एक नया वेरिएबल t = प्रस्तुत करें ,फिर पूरा किया टी 2 = , यानी

= टी 2 – 2. 4. प्रतिस्थापित करें और हल करें.

द्विघात समीकरण

5. प्रतिस्थापन पर लौटें और परिणामी समीकरणों को हल करें।

6. उत्तर लिखिए.

लोग एल्गोरिथम का अध्ययन कर रहे हैं।

ब्लैकबोर्ड पर छात्र एल्गोरिथम के अनुसार समीकरण हल करता है और शिक्षक की मदद से बाकी लोग नोटबुक में लिखते हैं। 4 6x 3 – 5x 2 – 38x

– 5x + 6 = 0.

समाधान।

6x 2 – 5x – 38 – 5/x + 6/x 2 = 0.

6(x 2 + 1/x 2) – 5(x + 1/x) – 38 = 0.

टी दर्ज करें: प्रतिस्थापन (एक्स + 1/एक्स) = टी। प्रतिस्थापन: (x 2 + 1/x 2) = t 2 - 2, हमारे पास है:

6t 2 – 5t – 50 = 0.

टी = -5/2 या टी = 10/3.

आइए वेरिएबल x पर वापस लौटें। विपरीत प्रतिस्थापन के बाद, हम दो परिणामी समीकरणों को हल करते हैं:

1) एक्स + 1/एक्स = -5/2;

एक्स 2 + 5/2 एक्स +1 = 0;

x = -2 या x = -1/2.

2) एक्स + 1/एक्स = 10/3;

x 2 – 10/3 x + 1 = 0;

एक्स = 3 या एक्स = 1/3.

उत्तर:-2; -1/2; 1/3; 3.

16वीं शताब्दी के इतालवी गणितज्ञ एन. टार्टाग्लिया, ए. फियोर, डी. कार्डानो और अन्य ने तीसरी और चौथी डिग्री के समीकरणों की समस्या में महान योगदान दिया, 1535 में ए. फियोर और एन के बीच एक वैज्ञानिक द्वंद्व हुआ। टार्टाग्लिया, जिस पर बाद वाले ने जीत हासिल की। 2 घंटे में उसने फियोर द्वारा प्रस्तावित 30 समस्याओं को हल कर दिया, और फियोर खुद टार्टाग्लिया द्वारा दी गई एक भी समस्या को हल नहीं कर सका।

. दोस्तों, मैं आज आपको एक और समीकरण पेश करना चाहता हूं; मैंने इसे ओजीई की तैयारी के लिए समस्याओं के संग्रह से लिया है।

((x + 1)(x + 4))((x + 2)(x + 3)) = 24,

(x 2 + 5x + 4)(x 2 + 5x + 6) = 24.

प्रतिस्थापन x 2 + 5x + 4 = t करने पर, हमें समीकरण प्राप्त होता है

t(t + 2) = 24, यह वर्ग है:

टी 2 + 2टी – 24 = 0.

टी = -6 या टी = 4.

विपरीत प्रतिस्थापन करने के बाद, हम आसानी से मूल समीकरण की जड़ें ढूंढ लेते हैं।

उत्तर:-5; 0.

नई परिस्थितियों में ज्ञान और कौशल का रचनात्मक हस्तांतरण।

पाठ की शुरुआत में, हमने इस तथ्य के बारे में बात की कि यदि किसी समीकरण में दोहराए जाने वाले तत्व हैं, तो आप चर प्रतिस्थापन विधि का उपयोग कर सकते हैं। हम अभी तक नहीं जानते कि त्रिकोणमितीय और अपरिमेय समीकरणों को कैसे हल किया जाए। आइए देखें कि यदि हम सरल त्रिकोणमितीय और अपरिमेय समीकरणों को हल करना जानते हैं तो क्या हम उन पर यह विधि लागू कर सकते हैं।कार्य 1:

निम्नलिखित समीकरणों में चर के परिवर्तन का नाम बताइए।कार्य 2:

कई समीकरण बनाएं, जिनका समाधान परिवर्तनीय प्रतिस्थापन विधि पर आधारित है।

उपसंहार।

तो दोस्तों, हमारा पाठ समाप्त हो गया है। आइए अपने पाठ को संक्षेप में प्रस्तुत करें।

पाठ की शुरुआत में हमने क्या लक्ष्य निर्धारित किए?

क्या हमारे लक्ष्य प्राप्त हो गये हैं?

गृहकार्य।

4x 4 – 8x 3 + 3x 2 – 8x + 4 = 0

(x+1)(x+2)(x+4)(x+5) = 40

. (इतालवी गणितज्ञों का समीकरण)

और मैं इस पाठ को महान वैज्ञानिक आइंस्टीन ए के शब्दों के साथ समाप्त करना चाहूँगा:

“मुझे अपना समय राजनीति और समीकरणों के बीच बांटना होगा। हालाँकि, मेरी राय में, समीकरण कहीं अधिक महत्वपूर्ण है, क्योंकि राजनीति केवल इस क्षण के लिए मौजूद है, और समीकरण हमेशा के लिए मौजूद रहेगा।

सबक के लिए धन्यवाद! अलविदा!

गणित एक छेद है जिसके माध्यम से तार्किक दिमाग आदर्श दुनिया में झाँक सकता है।

क्रोटोव विक्टर

स्कूल में, तर्कसंगत समीकरण बीजगणित पाठ्यक्रम में अग्रणी स्थान रखते हैं। किसी भी अन्य विषय की तुलना में उनके अध्ययन पर अधिक समय दिया जाता है। यह मुख्य रूप से इस तथ्य के कारण है कि समीकरणों का न केवल महत्वपूर्ण सैद्धांतिक महत्व है, बल्कि यह कई व्यावहारिक उद्देश्यों को भी पूरा करता है। बहुत बड़ी संख्यावास्तविक दुनिया की समस्याएं विभिन्न समीकरणों को हल करने के लिए आती हैं, और उन्हें हल करने के तरीकों में महारत हासिल करने के बाद ही आप विज्ञान और प्रौद्योगिकी के विभिन्न प्रश्नों के उत्तर पा सकेंगे।

तर्कसंगत समीकरणों को हल करने की क्षमता विकसित करने के लिए, छात्र का स्वतंत्र कार्य होता है बडा महत्व. हालाँकि, आगे बढ़ने से पहले स्वतंत्र कार्य, आपको हर चीज़ को स्पष्ट रूप से जानने और व्यवहार में लागू करने में सक्षम होने की आवश्यकता है संभावित तरीकेसमाधान तर्कसंगत समीकरण.

आइए उदाहरणों का उपयोग करके इसे विस्तार से देखें। परिवर्तनीय प्रतिस्थापन विधितर्कसंगत समीकरणों को हल करने के लिए.

उदाहरण 1.

समीकरण को हल करें (2x 2 – 3x + 1) 2 = 22x 2 – 33x + 1.

– 5x + 6 = 0.

आइए समीकरण को फॉर्म में फिर से लिखें

(2x 2 – 3x + 1) 2 = 11(2x 2 – 3x) + 1. आइए एक प्रतिस्थापन करें। मान लीजिए 2x 2 – 3x = t, तो समीकरण इस प्रकार बनेगा:

(t + 1) 2 = 11t + 1.

आइए अब कोष्ठक खोलें और समान दें, हमें मिलता है:

टी 2 + 2टी + 1 = 11टी + 1;

परिणामी अपूर्ण द्विघात समीकरण में, हम सामान्य गुणनखंड को कोष्ठक से बाहर निकालते हैं और हमारे पास होता है:

टी = 0 या टी = 9.

अब आपको एक विपरीत प्रतिस्थापन करने और प्रत्येक परिणामी समीकरण को हल करने की आवश्यकता है:

2x 2 – 3x = 0 या 2x 2 – 3x = 9

x(2x – 3) = 0 2x 2 – 3x – 9 = 0

x = 0 या x = 3/2 x = 3 या x = -3/2

उत्तर:-1.5; 0; 1.5; 3.

उदाहरण 2.

समीकरण (x 2 – 6x) 2 – 2(x – 3) 2 = 81 को हल करें।

– 5x + 6 = 0.

आइए वर्ग अंतर (a - b) 2 = a 2 - 2ab + b 2 के लिए सूत्र लागू करें। आइए मूल समीकरण को फॉर्म में लिखें

(x 2 – 6x) 2 – 2(x 2 – 6x + 9) = 81. अब आप प्रतिस्थापन कर सकते हैं।

मान लीजिए x 2 – 6x = t, तो समीकरण इस प्रकार दिखेगा:

टी 2 – 2(टी + 9) = 81.

टी 2 – 2टी – 18 – 81 = 0;

टी 2 – 2टी – 99 = 0.

विएटा के प्रमेय के अनुसार, परिणामी समीकरण की जड़ें संख्या -9 और 11 होंगी।

आइए एक उलटा प्रतिस्थापन करें:

x 2 – 6x = -9 या x 2 – 6x = 11

x 2 – 6x + 9 = 0 x 2 – 6x – 11 = 0

(x – 3) 2 = 0 डी = 80

एक्स = 3 एक्स 1 = 3 + 2√5; एक्स 2 = 3 – 2√5.

उत्तर: 3 – 2√5; 3; 3 + 2√5.

उदाहरण 3.

समीकरण (x – 1)(x – 3)(x + 5)(x + 7) = 297 को हल करें और इसके मूलों का गुणनफल ज्ञात करें।

– 5x + 6 = 0.

आइए कारकों को समूहीकृत करने और कोष्ठक के जोड़े खोलने का एक "लाभकारी" तरीका खोजें:

((x – 1)(x + 5))((x – 3)(x + 7)) = 297;

(x 2 + 5x – x – 5)(x 2 + 7x – 3x – 21) = 297;

(x 2 + 4x – 5)(x 2 + 4x – 21) = 297.

आइए प्रतिस्थापन x 2 + 4x = t करें, तो समीकरण इस तरह दिखेगा:

(t – 5)(t – 21) = 297.

आइए कोष्ठक खोलें और समान शब्द प्रस्तुत करें:

टी 2 – 21टी – 5टी + 105 = 297;

टी 2 – 26टी – 192 = 0.

विएटा के प्रमेय का उपयोग करते हुए, हम यह निर्धारित करते हैं कि परिणामी समीकरण की जड़ें संख्या -6 और 32 होंगी।

विपरीत प्रतिस्थापन के बाद हमारे पास होगा:

x 2 + 4x = -6 या x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x – 32 = 0

डी = 16 – 24< 0 D = 16 + 128 > 0

कोई मूल नहीं x 1 = -8; एक्स 2 = 4

आइए जड़ों का गुणनफल ज्ञात करें: -8 · 4 = -32.

उत्तर:-32.

उदाहरण 4.

समीकरण (x 2 – 2x + 2) 2 + 3x(x 2 – 2x + 2) = 10x 2 के मूलों का योग ज्ञात कीजिए।

– 5x + 6 = 0.

मान लीजिए x 2 – 2x + 2 = t, तो समीकरण इस प्रकार बनेगा:

टी 2 + 3xt – 10x 2 = 0.

आइए परिणामी समीकरण को t के संबंध में द्विघात मानें।

डी = (3x) 2 - 4 · (-10x 2) = 9x 2 + 40x 2 = 49x 2; ≥≤

t 1 = (-3x – 7x) / 2 और t 2 = (-3x + 7x) / 2;

टी 1 = -5x और टी 2 = 2x.

चूँकि t = x 2 – 2x + 2, तो

x 2 – 2x + 2 = -5x या x 2 – 2x + 2 = 2x. आइए प्रत्येक परिणामी समीकरण को हल करें।

x 2 + 3x + 2 = 0 या x 2 – 4x + 2 = 0.

दोनों समीकरणों की जड़ें हैं, क्योंकि डी > 0.

विएटा के प्रमेय का उपयोग करके, हम यह निष्कर्ष निकाल सकते हैं कि पहले समीकरण की जड़ों का योग -3 है, और दूसरे समीकरण की जड़ों का योग 4 है। हम पाते हैं कि मूल समीकरण की जड़ों का योग -3 + 4 = 1 है

उत्तर: 1.

उदाहरण 5.

समीकरण का मूल ज्ञात कीजिए (x + 1) 4 + (x + 5) 4 = 32, बीच [-5; 10].

– 5x + 6 = 0.

मान लीजिए x = t – 3, तो x + 1 = t – 2; x + 5 = t + 2 और मूल समीकरण इस प्रकार है:

(टी - 2) 4 + (टी + 2) 4 = 32। भावों को चौथी घात तक बढ़ाने के लिए, आप पास्कल के त्रिकोण का उपयोग कर सकते हैं (चित्र 1);

(टी - 2) 4 = टी 4 - 4टी 3 2 + 6टी 2 2 2 - 4टी 2 3 + 2 4 ;

(टी + 2) 4 = टी 4 + 4टी 3 2 + 6टी 2 2 2 + 4टी 2 3 + 2 4।

समान पदों को घटाने पर हमें प्राप्त होता है:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

टी 4 + 6टी 2 2 2 + 2 4 = 16;

टी 4 + 24टी 2 + 16 = 16;

टी 4 + 24टी 2 = 0;

टी 2 (टी 2 + 24) = 0;

टी = 0 या टी 2 = -24.

दूसरे समीकरण का कोई मूल नहीं है, जिसका अर्थ है विपरीत प्रतिस्थापन के बाद भी t = 0

एक्स = टी - 3 = 0 - 3 = -3. समीकरण -3 का मूल अंतराल [-5; 10]।

उत्तर:-3.

जैसा कि आप देख सकते हैं, तर्कसंगत समीकरणों को हल करते समय, आपको उपरोक्त सूत्रों को जानना होगा और सही ढंग से गिनने में सक्षम होना होगा। प्रतिस्थापन चुनते समय और रिवर्स प्रतिस्थापन के दौरान त्रुटियां अक्सर होती हैं। इससे बचने के लिए आपको प्रत्येक कार्य का विस्तार से वर्णन करना होगा, फिर आपके निर्णयों में कोई गलती नहीं होगी।

वेबसाइट, सामग्री को पूर्ण या आंशिक रूप से कॉपी करते समय, स्रोत के लिंक की आवश्यकता होती है।